The Secretary Problem

Optimal Stopping in Decision Theory

Vadim Sokolov

Introduction

• The Secretary Problem (marriage problem, sultan’s dowry problem).
• Classic problem in decision theory and probability.
• Scenario: Select the best candidate from \(T\) sequential offers.

The Rules

1. You receive \(T\) offers one by one.
2. You must accept or reject on the spot.
3. You cannot return to a previous offer.
4. Aim: Maximize the probability of choosing the absolute best.

The 37% Rule

• Strategy: Reject the first \(r\) candidates to gain information, then pick the next one better than all previous.
• Optimal \(r\): \(r \approx T/e \approx 0.37 T\).
• One should reject the first 37% of candidates and then select the first one who is better than all those seen so far.

Mathematical Background

• Principle of optimality (Richard Bellman).
• Probability of success: \[ \begin{aligned} P(\text{success}) &= \frac{r}{T} \sum_{a=r+1}^T \frac{1}{a-1} \\ &\approx \frac{r}{T} \int_{r}^{T} \frac{1}{x} dx = \frac{r}{T} \log \left( \frac{T}{r} \right) \end{aligned} \]
• Maximize \(f(x) = x \log(1/x) \implies x = 1/e \approx 0.37\).

Simulation in Python

import numpy as np
import matplotlib.pyplot as plt

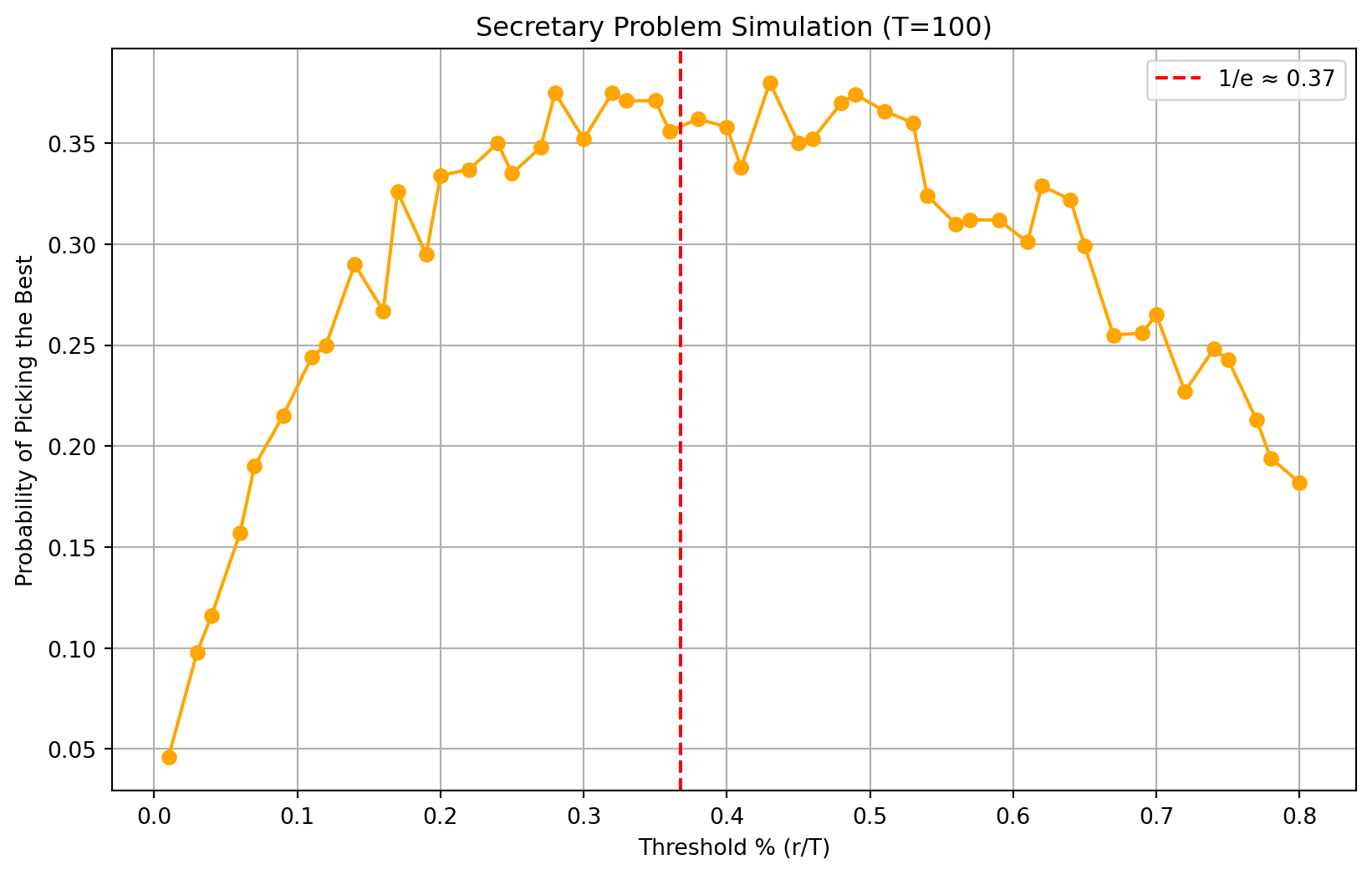
def secretary_simulation(n=100, nmc=1000):
    np.random.seed(17)
    rules = np.unique(np.round(n * np.linspace(0.01, 0.8, 50)).astype(int))
    rules = rules[rules > 0]
    
    success_rate = np.zeros(len(rules))
    
    for i, r in enumerate(rules):
        for _ in range(nmc):
            candidates = np.random.permutation(np.arange(1, n + 1))
            screen = candidates[:r]
            best_screen = np.max(screen) if len(screen) > 0 else 0
            choices = candidates[r:]
            selected = None
            for c in choices:
                if c > best_screen:
                    selected = c
                    break
            if selected is None:
                selected = candidates[-1]
            if selected == n:
                success_rate[i] += 1
    return rules, success_rate / nmc

rules, prob_best = secretary_simulation()

Simulation Results

plt.figure(figsize=(10, 6))
plt.plot(rules/100, prob_best, 'o-', color='orange')
plt.axvline(1/np.e, color='red', linestyle='--', label='1/e ≈ 0.37')
plt.xlabel('Threshold % (r/T)')
plt.ylabel('Probability of Picking the Best')
plt.title('Secretary Problem Simulation (T=100)')
plt.legend()
plt.grid(True)
plt.show()

Key Takeaways

• Balance exploration (the first 37%) and exploitation (choosing the first best).
• The maximum probability of success is also approximately 37%.
• This rule applies to many sequential decision-making scenarios.