Bodyfat Abdomen
1 12.3 85.2
2 6.1 83.0
3 25.3 87.9
4 10.4 86.4
5 28.7 100.0Bayes AI
Unit 5: Bayesian Regression: Linear and Bayesian Trees

Vadim Sokolov
George Mason University
Spring 2025
Bayesian Regression
\[ y_i \sim D(f(\eta_i),\theta) \]
- \(f\): inverse of the link function
- \(\eta_i\): linear predictor
- \(D\): distribution of the response variable (family) \[ \eta = X\beta + Zu \]
- \(\beta,u,\theta\): model parameters; \(\beta\) - fixed effects, \(u\) - random effects
The Problem - Predicting a Continuous Outcome
- We have data: \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\)
- \(x_i\) represents a set of features (predictors, independent variables). Could be a vector (e.g., \(x_i = [age, weight, height]\)).
- \(y_i\) is a continuous target variable (dependent variable, response). We want to predict \(y\) given \(x\).
- Example: Predicting house price (\(y\)) based on size, location, number of bedrooms (\(x\)).
The Linear Regression Model (Review)
We assume a linear relationship between \(x\) and \(y\):
\[ y_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \ldots + \beta_px_{ip} + \epsilon_i \]
- \(\beta_0, \beta_1, \ldots, \beta_p\) are the coefficients (parameters) we need to estimate. \(\beta_0\) is the intercept.
- \(x_{ij}\) is the \(j\)-th feature of the \(i\)-th data point.
- \(\epsilon_i\) is the error term, assumed to be normally distributed: \(\epsilon_i \sim N(0, \sigma^2)\)
- \(\sigma^2\) is the variance of the error (noise).
In matrix form: \(y = X\beta + \epsilon\)
From Frequentist to Bayesian
- Frequentist Approach (e.g., Ordinary Least Squares):
- Find the single best set of coefficients (\(\beta\)) that minimize the sum of squared errors.
- Coefficients (\(\beta\)) are treated as fixed, unknown constants.
- Bayesian Approach:
- Treat the coefficients (\(\beta\)) and the variance (\(\sigma^2\)) as random variables.
- We define prior distributions for \(\beta\) and \(\sigma^2\), representing our initial beliefs.
- We use Bayes’ Theorem to update these beliefs based on the data.
- We obtain posterior distributions for \(\beta\) and \(\sigma^2\), representing our updated beliefs.
Bayes’ Theorem - The Core
Bayes’ Theorem tells us how to update our beliefs:
\[ P(\theta | Data) = [ P(Data | \theta)P(\theta) ] / P(Data) \]
- \(P(\theta | Data):\) Posterior distribution - Our updated belief about the parameters () after seeing the data. This is what we want!
- \(P(Data | \theta):\) Likelihood function - The probability of observing the data given specific parameter values.
- \(P(\theta):\) Prior distribution - Our initial belief about the parameters before seeing the data.
- \(P(Data):\) Evidence (marginal likelihood) - The probability of the data (a normalizing constant). Often difficult to compute directly.
Bayesian Linear Regression - Example
- Likelihood: \(P(Data | \beta, \sigma^2)\)
- Since \(y = X\beta + \epsilon\) and \(\epsilon \sim N(0, \sigma^2)\):
- \(y_i | \beta, \sigma^2 \sim N(X_i\beta, \sigma^2)\) (The data is normally distributed around the predicted value.)
- The likelihood function is the product of these normal distributions for all data points.
- Priors: \(P(\beta, \sigma^2)\) (Often factored as \(P(\beta)P(\sigma^2)\) - assuming prior independence)
- For \(\beta\) (coefficients):
- Common choice: Normal prior: \(\beta \sim N(μ_0, Σ_0)\)
- \(μ_0\): Prior mean (vector). Often set to 0 (no prior preference for any particular coefficient value).
- \(Σ_0\): Prior covariance matrix. Controls the prior uncertainty. A diagonal matrix with large values means high uncertainty (a “weak” prior).
- Common choice: Normal prior: \(\beta \sim N(μ_0, Σ_0)\)
- For \(\sigma^2\) (variance):
- Common choice: Inverse Gamma prior: \(\sigma^2 \sim InvGamma(a, b)\)
- \(a\) and \(b\) are hyperparameters controlling the shape and scale of the distribution. Carefully chosen to be non-informative or weakly informative.
- Common choice: Inverse Gamma prior: \(\sigma^2 \sim InvGamma(a, b)\)
- For \(\beta\) (coefficients):
The Posterior Distribution
Applying Bayes’ Theorem:
\[ P(\beta, \sigma^2 | Data) \propto P(Data | \beta, \sigma^2)P(\beta)P(\sigma^2) \]
The posterior is proportional to the product of the likelihood and the priors.
Crucially: For certain choices of priors (like the Normal prior for \(\beta\) and Inverse Gamma for \(\sigma^2\)), the posterior has a known form (conjugate priors). This makes calculations easier. In other cases, we use approximation techniques.
Inference and Prediction
- Inference: We’re interested in the posterior distribution \(P(\beta, \sigma^2 | Data)\). This tells us:
- The most likely values of the coefficients (\(\beta\)).
- The uncertainty associated with these estimates (captured by the spread of the posterior). The uncertainty in the noise variance (\(\sigma^2\)).
- Prediction: Given a new input \(x^*\), we want to predict the corresponding output \(y^*\).
We use the posterior predictive distribution: \(P(y^* | x^*, Data)\)
This distribution integrates over the posterior distribution of the parameters:
\[ P(y^* | x^*, Data) = ∫ P(y^* | x^*, \beta, \sigma^2)P(\beta, \sigma^2 | Data) d\beta d\sigma^2 \]
This gives us a distribution over possible values of \(y^*\), not just a single point estimate. This captures the uncertainty in our prediction.
Advantages of Bayesian Linear Regression
- Uncertainty Quantification: Provides a full probability distribution over the parameters and predictions, not just point estimates. This is crucial for decision-making.
- Incorporation of Prior Knowledge: Allows us to incorporate prior beliefs about the parameters. This can be helpful when data is scarce or when we have expert knowledge.
- Regularization: The prior acts as a natural regularizer, preventing overfitting (especially with informative priors). Similar in effect to ridge regression or lasso.
- Model Comparison: Bayesian methods provide a framework for comparing different models (e.g., different sets of features) using the evidence (marginal likelihood).
Disadvantages and Challenges
- Computational Complexity: Calculating the posterior (especially the evidence) can be computationally expensive, especially for complex models and large datasets. Approximation techniques like Markov Chain Monte Carlo (MCMC) are often required.
- Prior Specification: Choosing appropriate priors can be challenging. Poorly chosen priors can lead to biased results. Sensitivity analysis (checking how the results change with different priors) is important.
- Interpretation: While uncertainty quantification is a strength, interpreting posterior distributions can sometimes be less intuitive than interpreting point estimates.
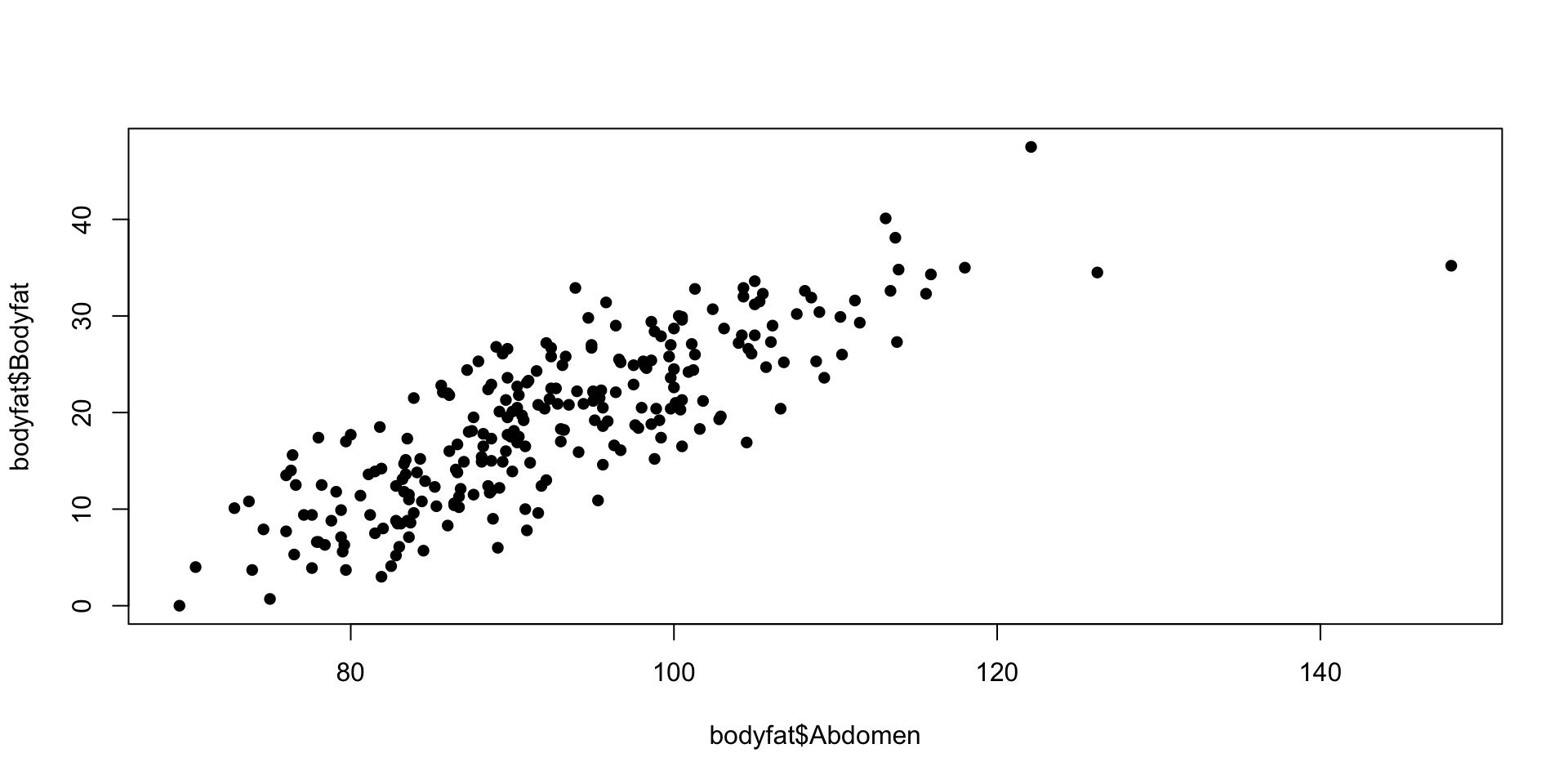
bodyfat example
- Body fat is hard to measure
- Can be predicted from abdominal circumference?
- Use The data set bodyfat can be found from the library BAS.
Classical Linear Regression
\[ y_i = \alpha + \beta x_i + \epsilon_i, \quad i = 1,\cdots, 252. \]
Call:
lm(formula = Bodyfat ~ Abdomen, data = bodyfat)
Residuals:
Min 1Q Median 3Q Max
-19.0160 -3.7557 0.0554 3.4215 12.9007
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -39.28018 2.66034 -14.77 <2e-16 ***
Abdomen 0.63130 0.02855 22.11 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.877 on 250 degrees of freedom
Multiple R-squared: 0.6617, Adjusted R-squared: 0.6603
F-statistic: 488.9 on 1 and 250 DF, p-value: < 2.2e-16Classical Linear Regression
Bayesian Simple Linear Regression Using the Reference Prior
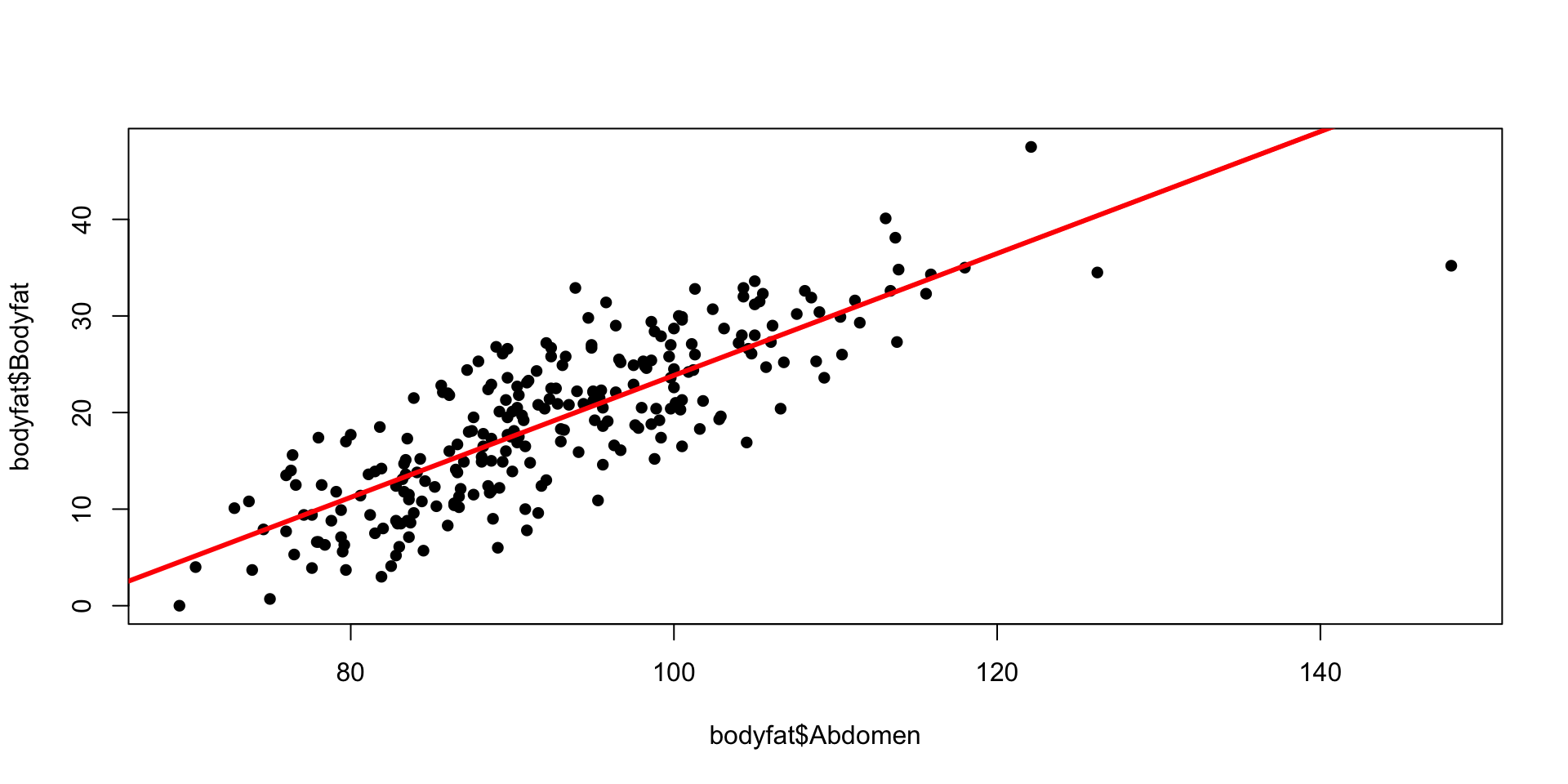
Likelihood: \[ Y_i~|~x_i, \alpha, \beta,\sigma^2~ \sim~ \textsf{Normal}(\alpha + \beta x_i, \sigma^2),\qquad i = 1,\cdots, n. \] Priors: \[ p(\alpha,\beta \mid \sigma^2) \propto 1, \quad p(\sigma^2) \propto 1/\sigma^2. \] Posterior: \[ \beta~|~y_1,\cdots,y_n ~\sim~ \textsf{t}\left(n-2,\ \hat{\beta},\ \frac{\hat{\sigma}^2}{\text{S}_{xx}}\right) = \textsf{t}\left(n-2,\ \hat{\beta},\ (\text{se}_{\beta})^2\right) \] \(\hat{\beta}\) and \(\hat{\beta},\ (\text{se}_{\beta})^2\) are MLE estimates! For derivation, see Section 6.1.4 of An Introduction to Bayesian Thinking
The Bayesian posterior credible intervals for \(\alpha\) and \(\beta\) under the reference prior, are numerically equivalent to the confidence intervals from the classical frequentist OLS analysis!
Plot
Code
ind = order(bodyfat$Abdomen)
x = bodyfat$Abdomen[ind]
df = data.frame(Abdomen = x)
ymean = predict(bodyfat.lm, newdata = df, interval = "confidence")
ypred = predict(bodyfat.lm, newdata = df, interval = "prediction")
plot(bodyfat$Abdomen, bodyfat$Bodyfat, pch=16)
lines(x, ymean[,1], col="red", lwd=3)
lines(x, ymean[,2], col="grey", lty=2)
lines(x, ymean[,3], col="grey", lty=2)
lines(x, ypred[,2], col="blue", lty=2)
lines(x, ypred[,3], col="blue", lty=2)
labels = c("Data", "Mean", "Confidence", "Prediction")
legend("topleft", legend = labels, col = c("black", "red", "grey", "blue"), lty = c(NA, 1, 2, 2), lwd = c(NA, 3, 1, 1))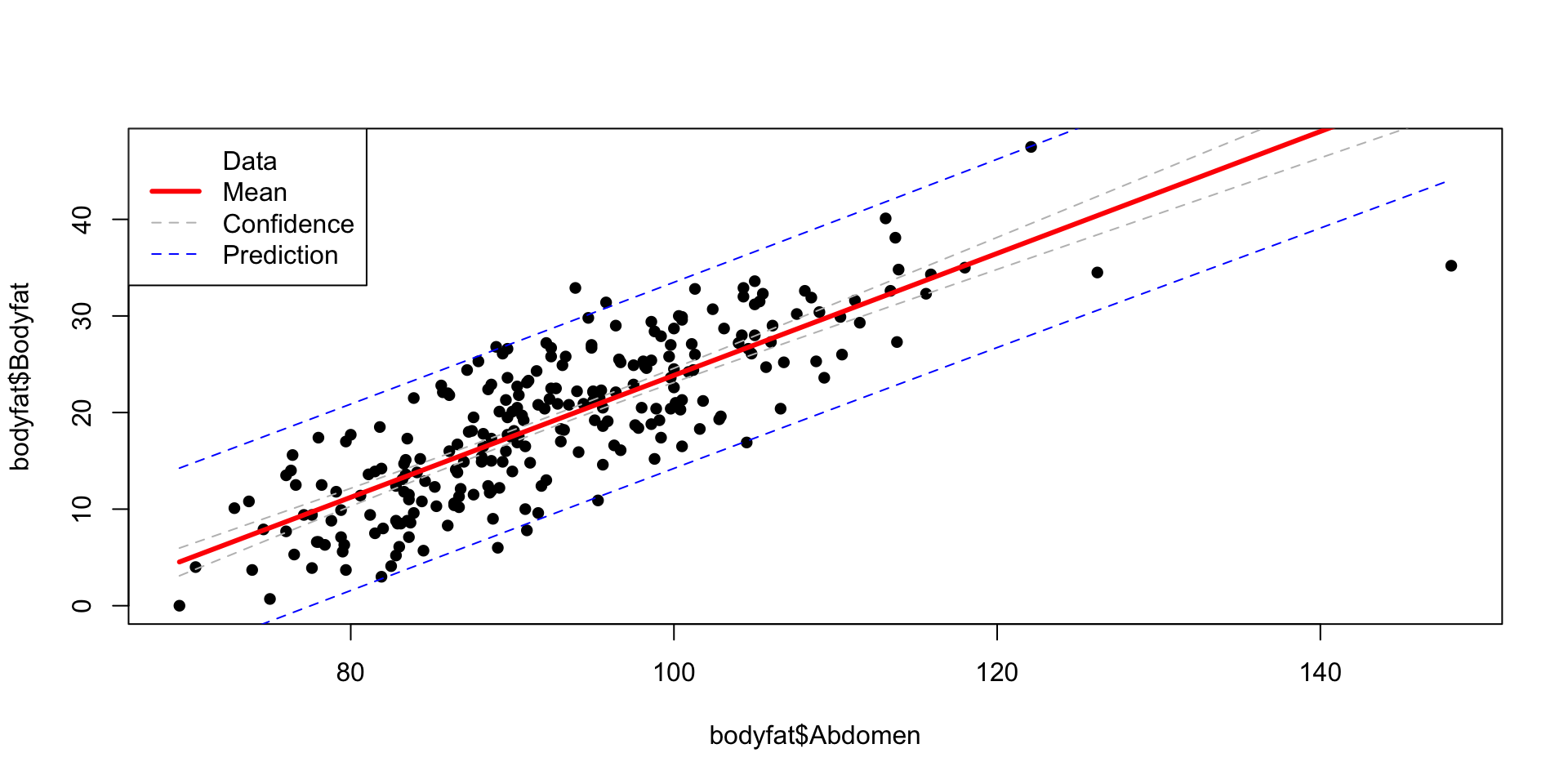
Informative Priors
Code
library(brms)
priors <- c(
prior(normal(0, 10), class = "b"), # Prior for coefficients (slope)
prior(normal(0, 25), class = "Intercept"), # Prior for the intercept
prior(student_t(3, 0, 100), class = "sigma") # Prior for the residual standard deviation
)
bodyfat.brms = brm(Bodyfat ~ Abdomen, data = bodyfat,family = gaussian(),prior = priors)
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 3.7e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.37 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.017 seconds (Warm-up)
Chain 1: 0.013 seconds (Sampling)
Chain 1: 0.03 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 3e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.018 seconds (Warm-up)
Chain 2: 0.012 seconds (Sampling)
Chain 2: 0.03 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 2e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.02 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.017 seconds (Warm-up)
Chain 3: 0.011 seconds (Sampling)
Chain 3: 0.028 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 2e-06 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.02 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.017 seconds (Warm-up)
Chain 4: 0.013 seconds (Sampling)
Chain 4: 0.03 seconds (Total)
Chain 4: Summary
Family: gaussian
Links: mu = identity; sigma = identity
Formula: Bodyfat ~ Abdomen
Data: bodyfat (Number of observations: 252)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
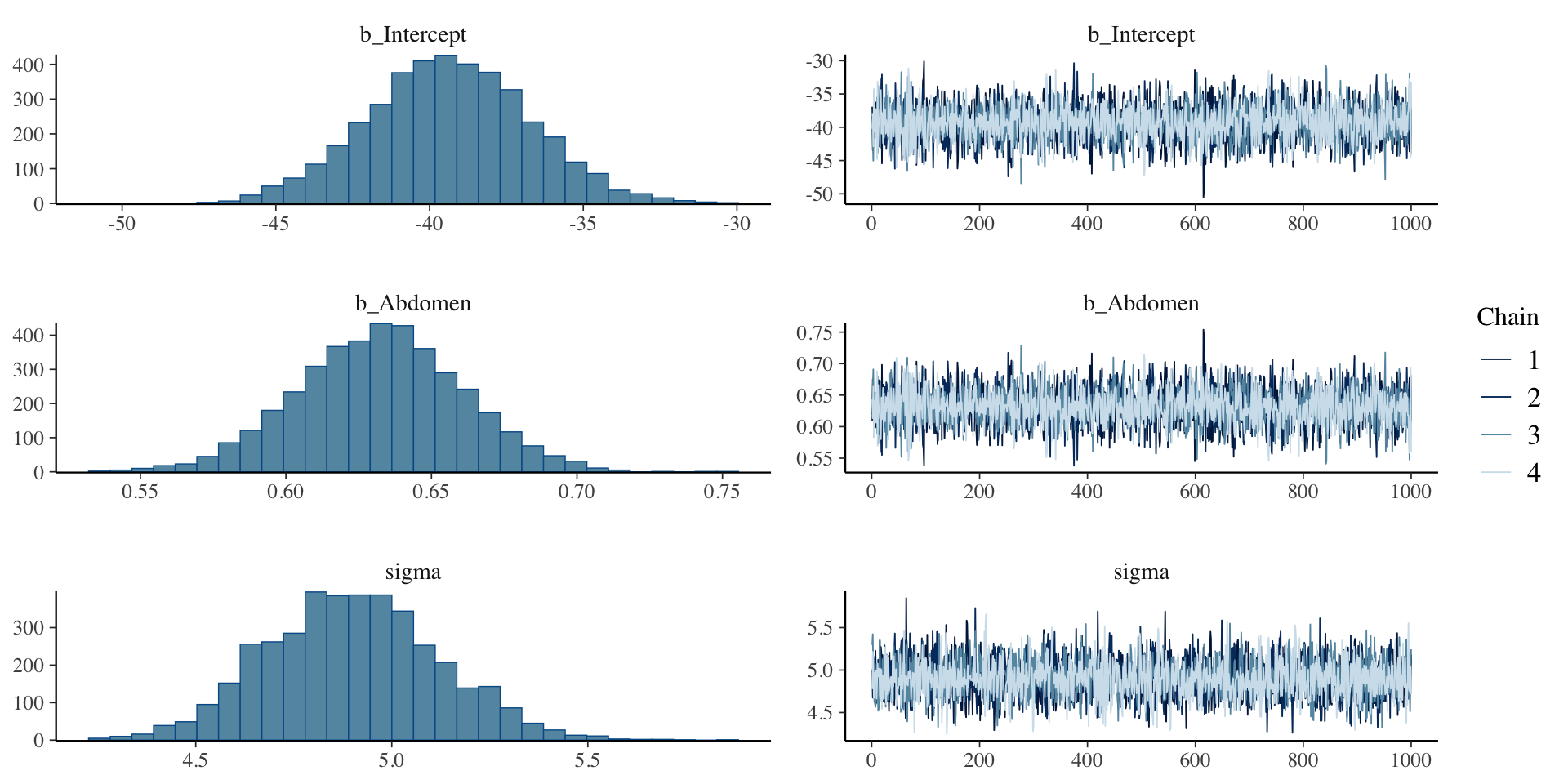
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept -39.38 2.65 -44.59 -34.24 1.00 4337 3061
Abdomen 0.63 0.03 0.58 0.69 1.00 4313 3114
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 4.90 0.22 4.48 5.34 1.00 4381 3053
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).Plot
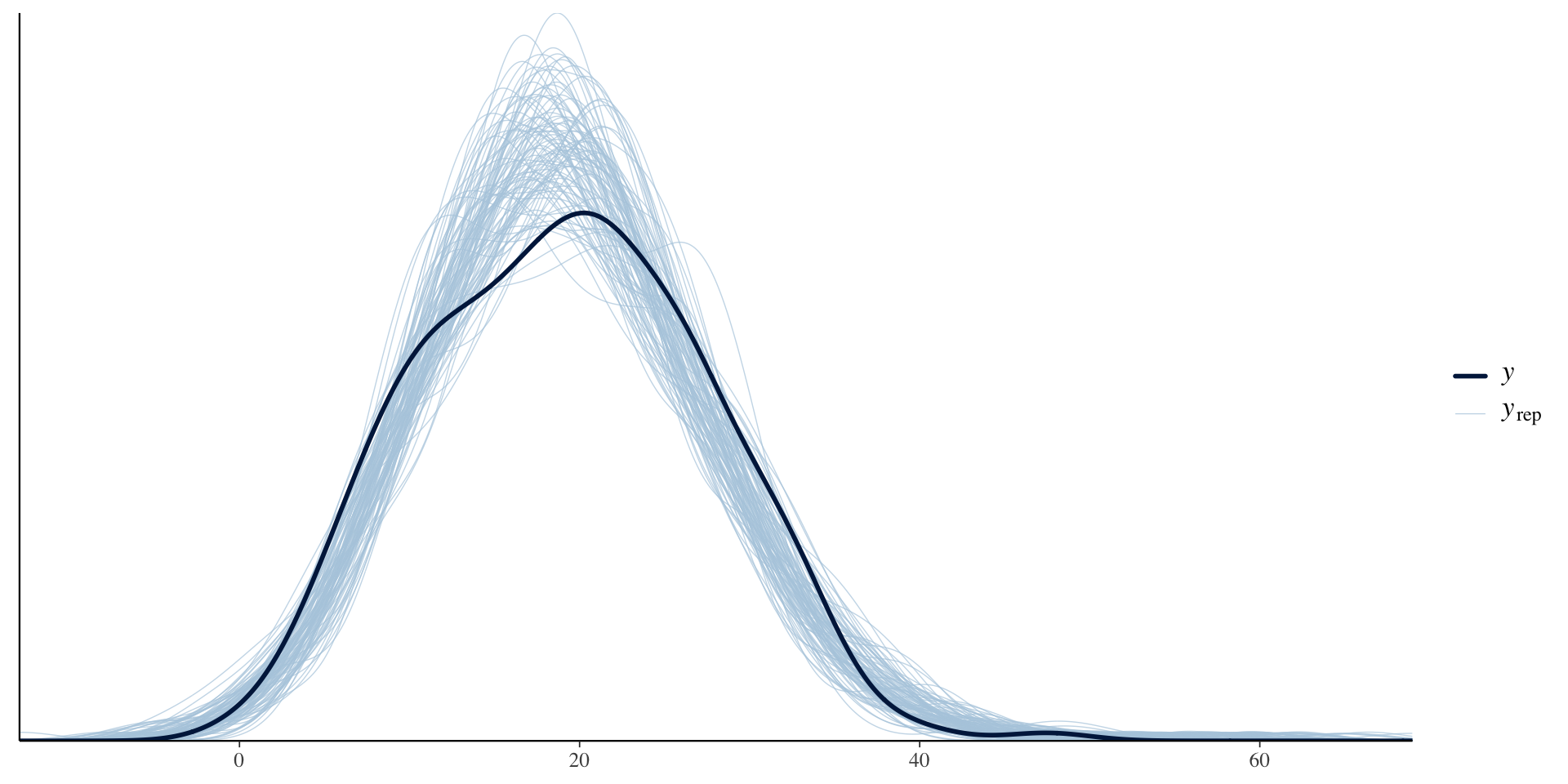
Plot all parameters
Plot Predictions
Code
new_data = data.frame(Abdomen = x)
predictions = posterior_predict(bodyfat.brms, newdata = new_data)
quntiles = apply(predictions, 2, function(x) quantile(x, c(0.025, 0.5,0.975)))
plot(bodyfat$Abdomen, bodyfat$Bodyfat, pch=16)
lines(x, quntiles[1,], col = "blue", lty = 2)
lines(x, quntiles[3,], col = "blue", lty = 2)
lines(x, quntiles[2,], col = "red", lwd = 3)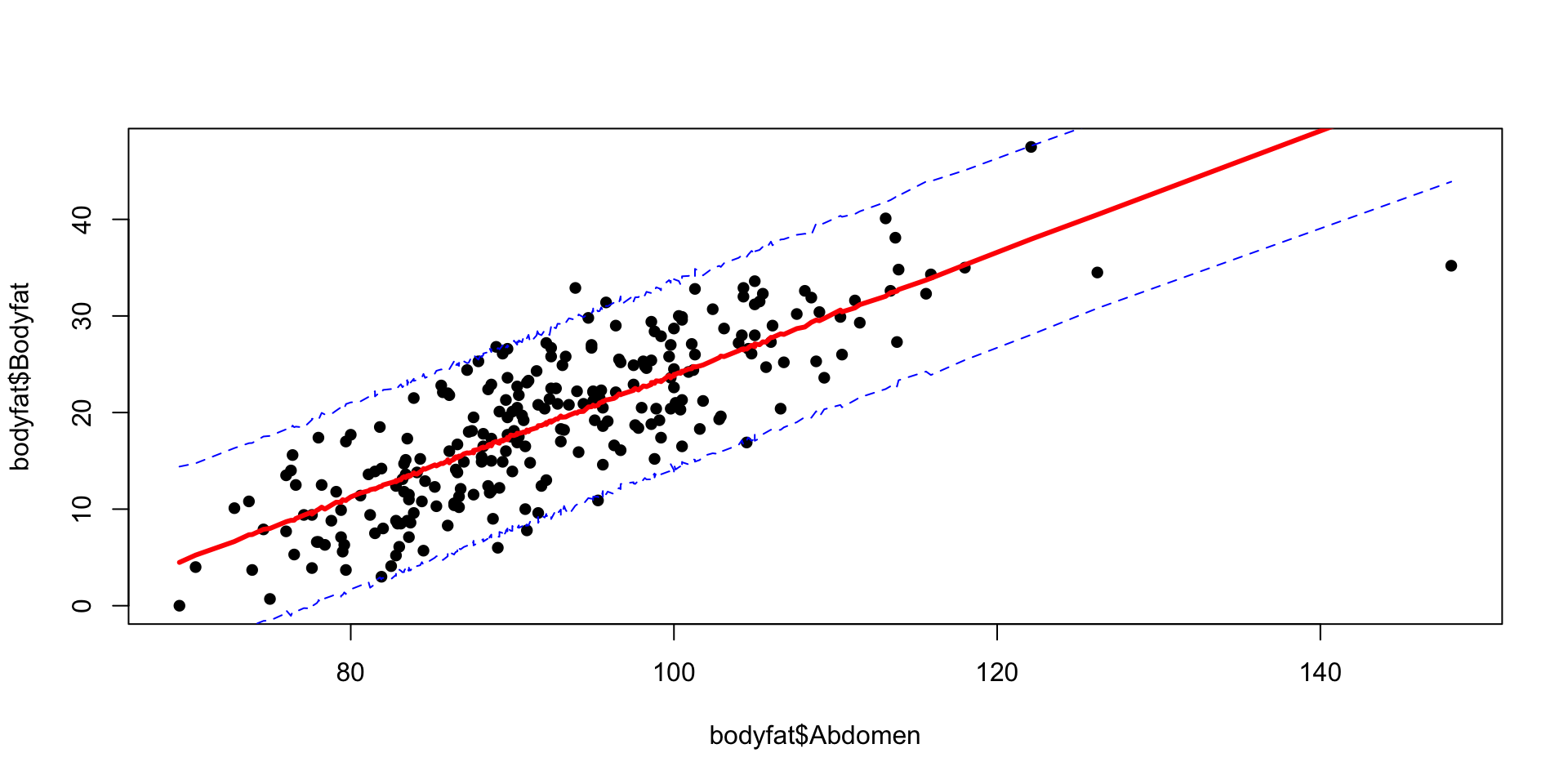
Small Data Example
Code
set.seed(7)
true_intercept <- 5
true_slope <- 2
true_sigma <- 3
# Number of data points (intentionally small)
n_data <- 15
# Generate predictor (x)
x <- runif(n_data, min = -5, max = 5)
# Generate outcome (y) with noise
y <- true_intercept + true_slope * x + rnorm(n_data, mean = 0, sd = true_sigma)
# Combine into a data frame
sim_data <- data.frame(x = x, y = y)
plot(x, y, pch = 16)
Classical Linear Regression
Call:
lm(formula = y ~ x, data = sim_data)
Residuals:
Min 1Q Median 3Q Max
-6.0837 -1.5346 -0.8869 1.9904 4.4709
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.5984 0.7468 4.818 0.000336 ***
x 1.6563 0.2350 7.047 8.71e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.795 on 13 degrees of freedom
Multiple R-squared: 0.7925, Adjusted R-squared: 0.7766
F-statistic: 49.66 on 1 and 13 DF, p-value: 8.712e-06Code
x_vals <- seq(min(sim_data$x), max(sim_data$x), length.out = 100)
# Get OLS predictions
ols_predictions <- predict(ols_model, newdata = data.frame(x = x_vals), interval = "confidence")
ols_predictions <- as.data.frame(ols_predictions) # Convert to data frame
ols_predictions$x <- x_vals
plot(x, y, pch = 16)
lines(x_vals,ols_predictions$fit)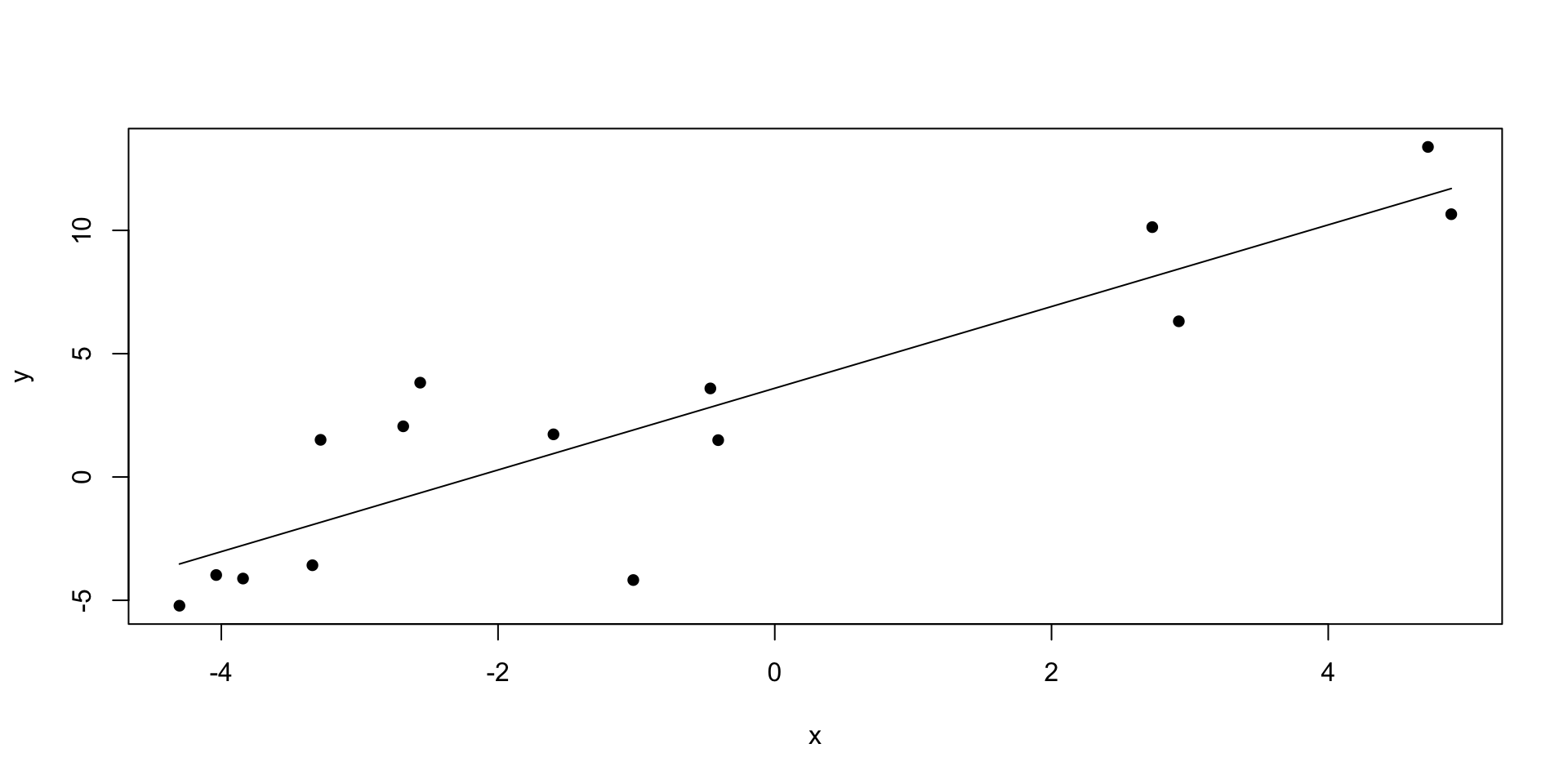
Bayesian Linear Regression
Code
priors <- c(
prior(normal(5, 1), class = "Intercept"), # Prior for intercept
prior(normal(2, 1), class = "b"), # Prior for slope
prior(student_t(3, 0, 5), class = "sigma") # Prior for sigma (wider than the true value)
)
# Fit the Bayesian model using brms
bayes_model <- brm(y ~ x,data = sim_data,family = gaussian(),prior = priors,seed = 123)
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 4.4e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.44 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.013 seconds (Warm-up)
Chain 1: 0.01 seconds (Sampling)
Chain 1: 0.023 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 4e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.013 seconds (Warm-up)
Chain 2: 0.011 seconds (Sampling)
Chain 2: 0.024 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 2e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.02 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.013 seconds (Warm-up)
Chain 3: 0.011 seconds (Sampling)
Chain 3: 0.024 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 2e-06 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.02 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.015 seconds (Warm-up)
Chain 4: 0.01 seconds (Sampling)
Chain 4: 0.025 seconds (Total)
Chain 4: Summary
Family: gaussian
Links: mu = identity; sigma = identity
Formula: y ~ x
Data: sim_data (Number of observations: 15)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 4.71 0.73 3.36 6.20 1.00 2856 2479
x 1.68 0.26 1.16 2.21 1.00 2984 2130
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 3.22 0.72 2.17 5.00 1.00 2474 2322
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).Plot
[1] "Bayesian Estimates:" Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 4.712777 0.7325443 3.358504 6.198919 1.001263 2855.809 2478.723
x 1.680288 0.2634961 1.161723 2.207987 1.001100 2984.003 2129.753Code
# Get Bayesian predictions (posterior draws of the expected value, epred)
bayes_predictions <- posterior_epred(bayes_model, newdata = data.frame(x = x_vals))
quntiles = apply(bayes_predictions, 2, function(x) quantile(x, c(0.025, 0.5,0.975)))
bayes_pred_summary= as.data.frame(t(quntiles)) #col.names=c("lwr","med","upr")
colnames(bayes_pred_summary) = c("lower","med","upper")
bayes_pred_summary$x <- x_vals
# Plot the data, OLS fit, and Bayesian fit
ggplot(sim_data) +
geom_point(aes(x = x, y = y),size = 3) +
# True regression line (for comparison)
geom_abline(intercept = true_intercept, slope = true_slope, color = "black", linetype = "dashed") +
# OLS regression line and confidence interval
geom_line(data = ols_predictions, aes(x = x, y = fit), color = "red") +
geom_ribbon(data = ols_predictions, aes(x=x, ymin = lwr, ymax = upr), fill = "red", alpha = 0.2) +
# Bayesian regression line and credible interval
geom_line(data = bayes_pred_summary, aes(x = x, y = med), color = "blue") +
geom_ribbon(data = bayes_pred_summary, aes(x=x, ymin = lower, ymax = upper), fill = "blue", alpha = 0.2) +
labs(title = "Bayesian vs. OLS Regression (Small Sample Size)",
x = "Predictor (x)",
y = "Outcome (y)") +
theme_bw()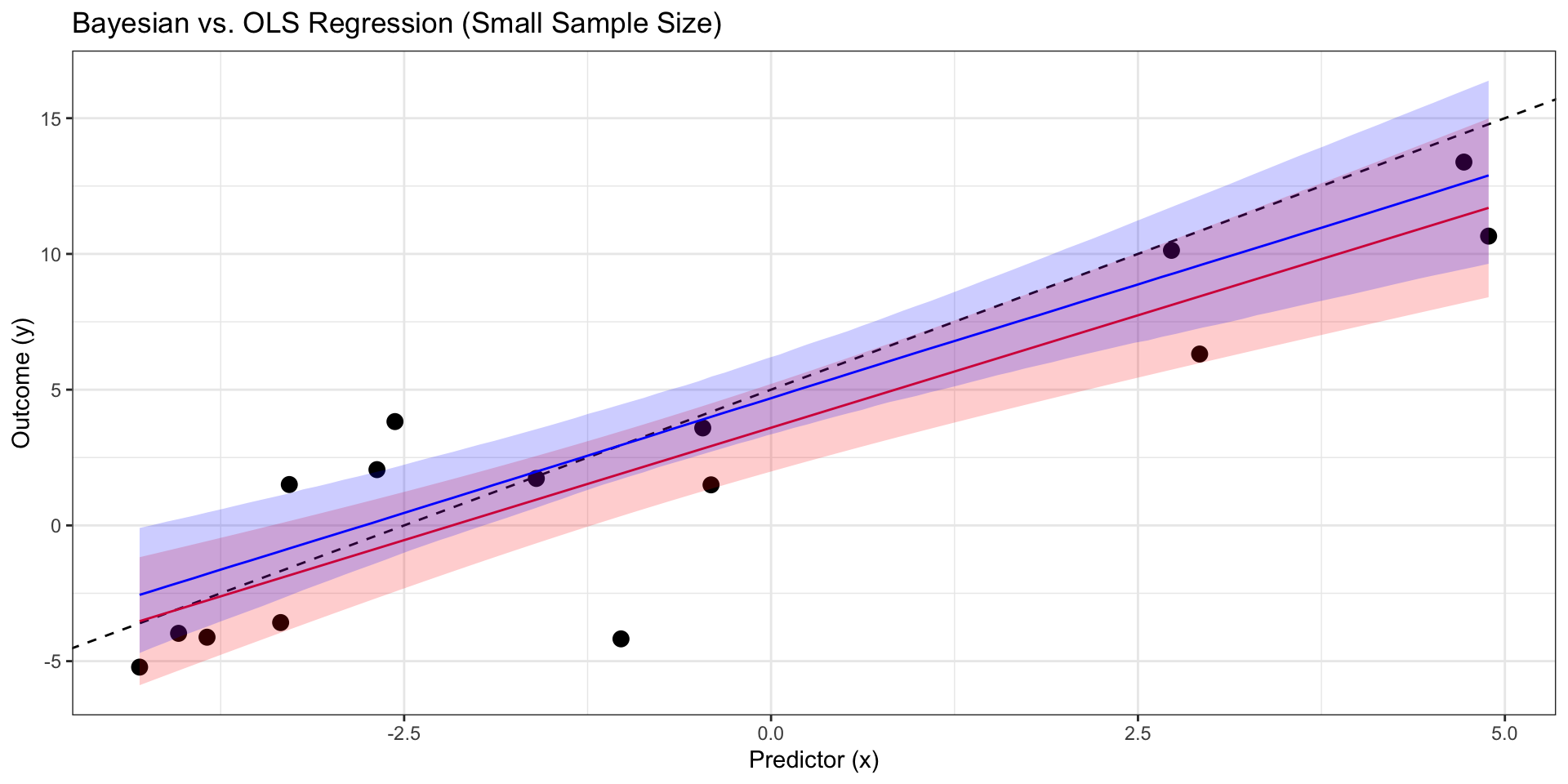
Sparsity Inducing Prior
Code
# Simulate data with some true coefficients and some noise
set.seed(7) # For reproducibility
n <- 100 # Number of observations
p <- 20 # Number of predictors (some relevant, some not)
true_beta <- c(5, -3, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) # Only first 3 are truly non-zero
X <- matrix(rnorm(n * p), n, p)
y <- X %*% true_beta + rnorm(n, 0, 5) # Adding noise
# Fit a standard linear regression (OLS)
ols_model <- lm(y ~ X-1)
# Fit a Bayesian linear regression with shrinkage (using the 'BAS' package)
# Install if you don't have it: install.packages("BAS")
library(BAS)
# Define prior (we'll use a g-prior which is common for shrinkage)
# 'gprior' is common for shrinkage
# 'bic' is another option that often works well
# 'hyper-g' is another good choice
bas_model <- bas.lm(y ~ X-1, prior = "g-prior", modelprior = uniform())
# Examine coefficients
ols_coef <- coef(ols_model)
bas_coef <- coefficients(bas_model) # These are *posterior means*
# Plot the coefficients to visualize shrinkage
plot(1:p, true_beta, type = "h", ylab = "Coefficient Value", xlab = "Predictor", main = "True Coefficients")
points(1:p, ols_coef, col = "red", pch = 16) # OLS
points(1:p, bas_coef$postmean, col = "blue", pch = 16) # Bayesian
abline(h = 0, lty = 2)
legend("topright", legend = c("True", "OLS", "Bayesian"), col = c("black", "red", "blue"), pch = 16)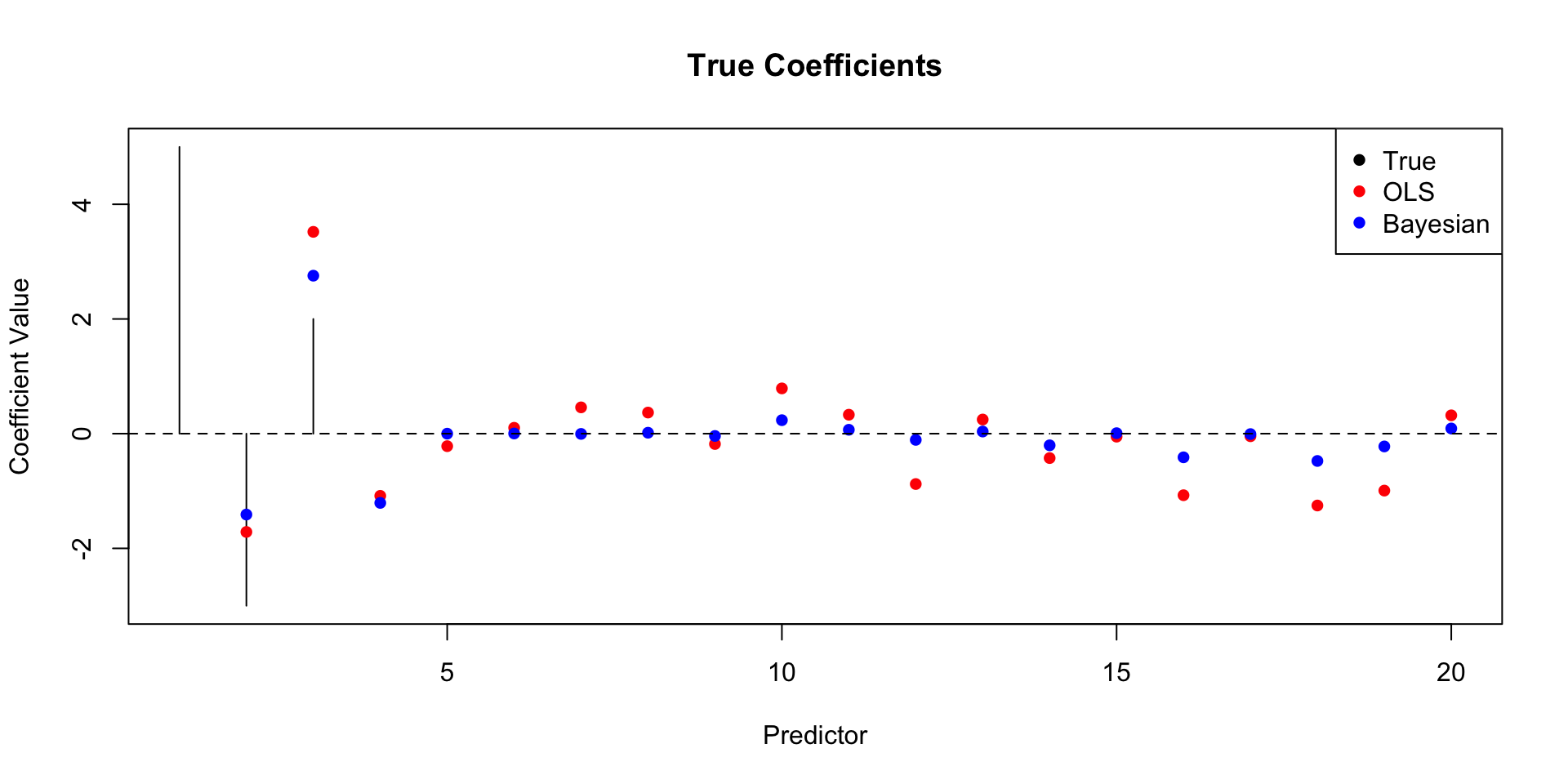
What are Random Intercepts Models?
- Extension of Linear Regression: Deals with clustered or hierarchical data.
- Clustered Data: Observations are grouped within clusters (e.g., students within schools, patients within hospitals, measurements over time within individuals).
- Problem with Standard Regression: Ignores the clustering, leading to:
- Underestimated standard errors (and thus, inflated Type I error rates - false positives).
- Incorrect conclusions about the significance of predictors.
- Random Intercepts: Assume each cluster has its own intercept, which is drawn from a distribution (usually normal). This accounts for between-cluster variability.
The Model Equation
Level 1 (Individual Level):
\[ y_{ij} = \beta_{0j} + \beta_1x_{ij} + \epsilon_{ij} \]
- \(y_{ij}\): Outcome for individual \(i\) in cluster \(j\).
- \(x_{ij}\): Predictor for individual \(i\) in cluster \(j\).
- \(\beta_{0j}\): Intercept for cluster \(j\).
- \(\beta_1\): Effect of \(x\) (assumed to be fixed - the same across all clusters).
- \(\epsilon_{ij}\): Individual-level error, \(\epsilon_{ij} \sim N(0, \sigma^2_e)\).
Level 2 (Cluster Level)
\[ \beta_{0j} = \gamma + u_{j} \]
\(\gamma\): Overall average intercept.
\(u_{j}\): Random effect (deviation) of cluster \(j\)’s intercept from the overall average, \(u_{j} \sim N(0, \sigma^2_u)\).
Combined Equation:
\[ y_{ij} = (\gamma+ u_{j}) + \beta_1x_{ij} + \epsilon_{ij} \]
Key Parameters & Interpretation
- \(\gamma\) (Fixed Intercept): The average outcome when the predictor \(x\) is zero (and across all clusters).
- \(\beta_1\) (Fixed Slope): The change in the outcome for a one-unit increase in \(x\), within any given cluster.
- \(\sigma^2_u\) (Random Intercept Variance): The variance of the cluster-specific intercepts. Indicates the amount of between-cluster variability. A larger \(\sigma^2_u\) means more variation between clusters.
- \(\sigma^2_e\) (Residual Variance): The variance of the individual-level errors. Indicates within-cluster variability.
- Intraclass Correlation Coefficient (ICC):
- \(ICC = \sigma^2_u / (\sigma^2_u + \sigma^2_e)\)
- Represents the proportion of total variance that is due to between-cluster differences. Ranges from 0 to 1. Higher ICC means more clustering.
Example: Student Test Scores in Schools
- Data: We have data on student test scores (\(score\)) and a student-level predictor (e.g., hours of study, \(studyhours\)). Students are nested within schools.
- Research Question: Does the number of study hours predict test scores, accounting for the fact that students are clustered within schools?
- Model:
- \(score_{ij} = \gamma + \beta_1(studyhours)_{ij} + u_{j} + \epsilon_{ij}\)
- \(u_{j} \sim N(0, \sigma^2_u)\)
- \(\epsilon_{ij} \sim N(0, \sigma^2_e)\)
R Demonstration - Setup and Data
Code
# Install and load necessary packages
library(lme4)
library(lmerTest)
library(ggplot2)
# Create some simulated data (for reproducibility)
set.seed(123)
n_schools <- 30 # Number of schools
n_students_per_school <- 20 # Students per school
n_total <- n_schools * n_students_per_school
school_effects <- rnorm(n_schools, mean = 0, sd = 2) # School random effects
student_data <- data.frame(
school_id = rep(1:n_schools, each = n_students_per_school),
studyhours = rnorm(n_total, mean = 10, sd = 3),
error = rnorm(n_total, mean=0, sd = 1)
)
# Generate scores based on the model
student_data$score <- 50 + 1.5 * student_data$studyhours +
school_effects[student_data$school_id] + student_data$error
head(student_data) school_id studyhours error score
1 1 11.279393 -0.6785031 65.11963
2 1 9.114786 -1.8555717 60.69566
3 1 12.685377 0.5332594 68.44037
4 1 12.634400 0.3102303 68.14088
5 1 12.464743 -1.3538343 66.22233
6 1 12.065921 -1.9429564 65.03497Plot
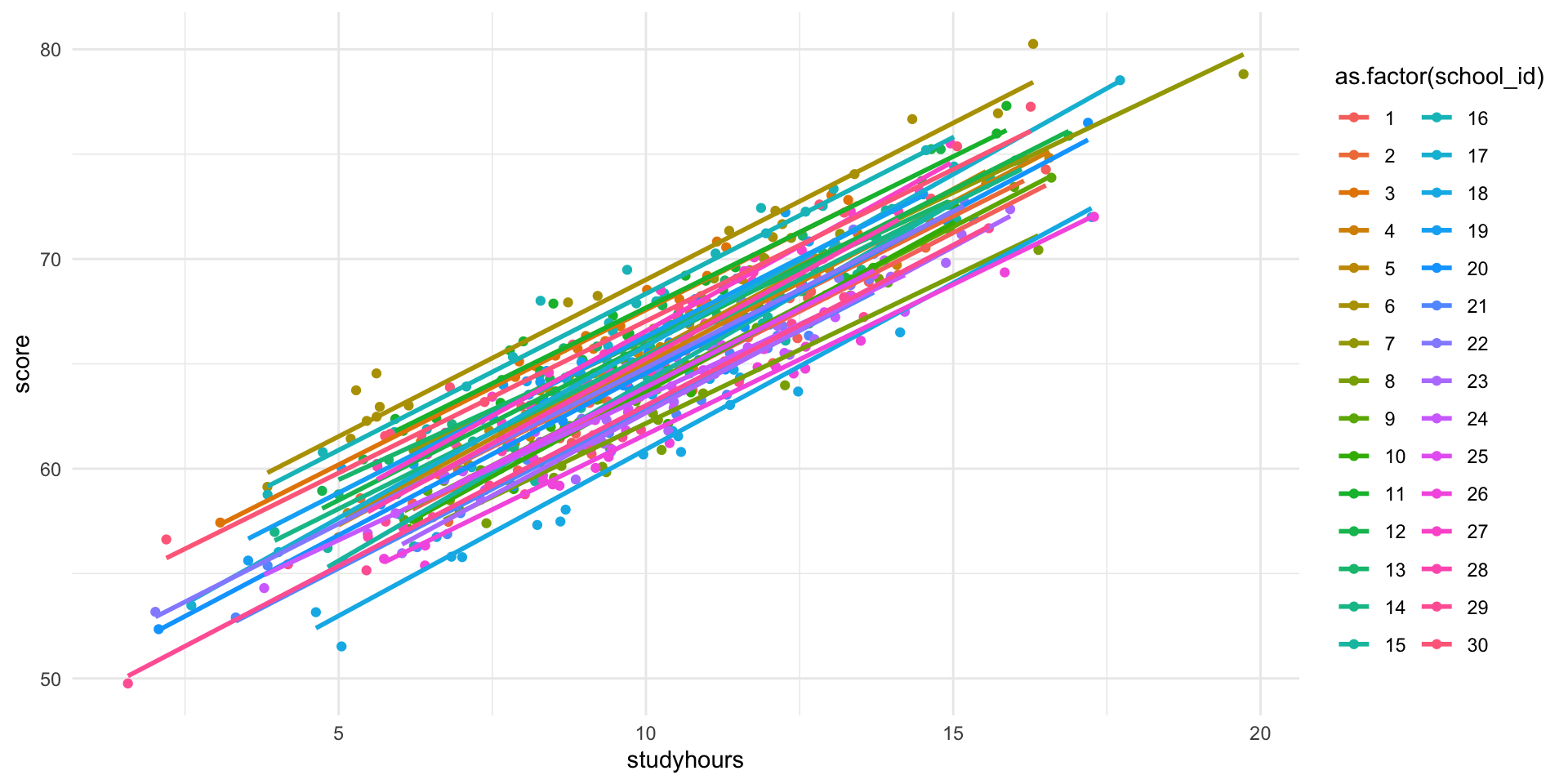
R Demonstration - Fit the Model
Code
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: score ~ studyhours + (1 | school_id)
Data: student_data
REML criterion at convergence: 1846.4
Scaled residuals:
Min 1Q Median 3Q Max
-2.71647 -0.68621 0.01679 0.64918 2.99847
Random effects:
Groups Name Variance Std.Dev.
school_id (Intercept) 3.845 1.961
Residual 1.014 1.007
Number of obs: 600, groups: school_id, 30
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 49.84593 0.38800 38.91559 128.5 <2e-16 ***
studyhours 1.50785 0.01432 569.50545 105.3 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
studyhours -0.371R Demonstration - Interpreting the Output
- Fixed Effects:
- Intercept \((\gamma)\): Estimated average score when \(studyhours\) is 0.
- studyhours \((\beta_1)\): Estimated increase in score for each additional hour of study. The p-value indicates if this effect is statistically significant.
- Random Effects:
- Variance (school_id) \(\sigma^2_u\): Estimated variance of the school-specific intercepts.
- Variance (Residual) \(\sigma^2_e\): Estimated variance of the individual-level errors.
ICC Calculation*
R Demonstration - Visualizing the Model
Code
# Get predicted values for each student
student_data$predicted <- predict(model)
# Plot observed vs. predicted values, colored by school
ggplot(student_data, aes(x = score, y = predicted, color = factor(school_id))) +
geom_point() +
geom_abline(intercept = 0, slope = 1, linetype = "dashed") + # Add a diagonal line
labs(title = "Observed vs. Predicted Scores",
x = "Observed Score",
y = "Predicted Score",
color = "School ID") +
theme_bw() +
theme(legend.position = "none") #remove legend because too many schools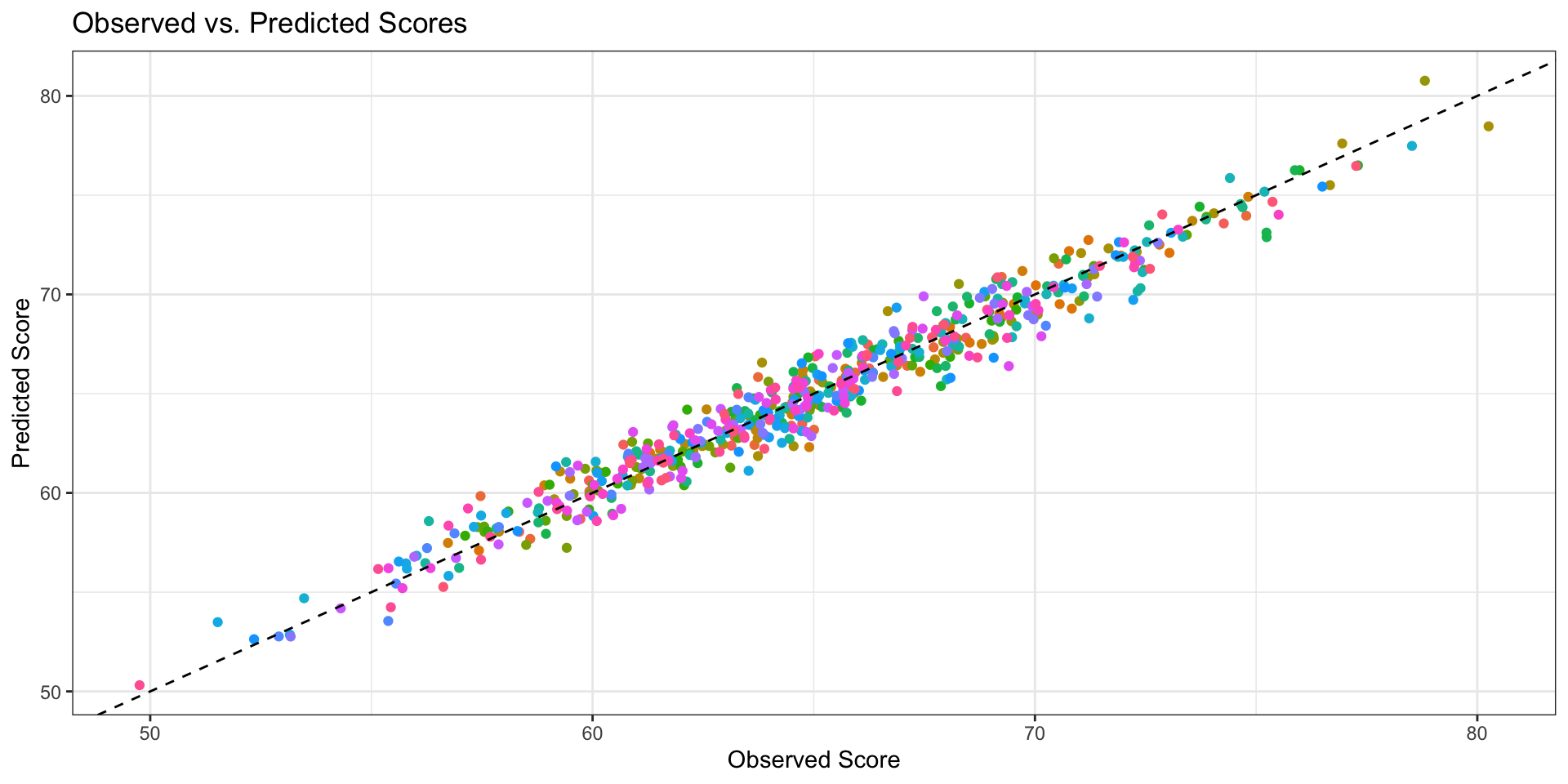
Plot random intercepts for each school
Plot random intercepts for each school
Code
ranef_df <- as.data.frame(ranef(model)$school_id)
ranef_df$school_id <- 1:nrow(ranef_df)
ggplot(ranef_df, aes(x = school_id, y = `(Intercept)`)) +
geom_point() +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(title = "Random Intercepts by School",
x = "School ID",
y = "Random Intercept (Deviation from Overall Mean)") +
theme_bw()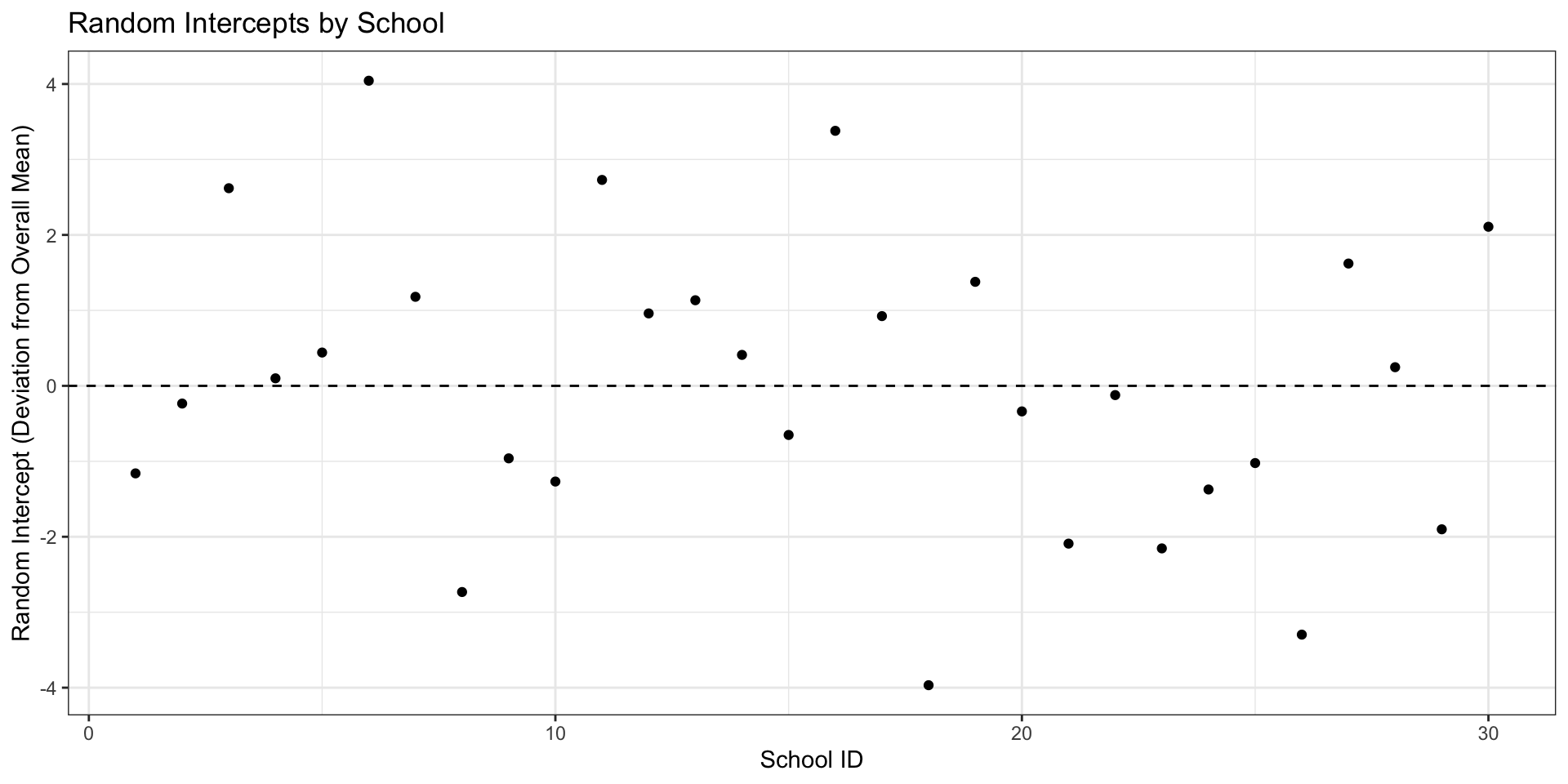
Comparing to a Simple Linear Model
Code
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 49.845931 0.38799971 38.91559 128.4690 9.116905e-53
studyhours 1.507846 0.01431791 569.50545 105.3119 0.000000e+00 Estimate Std. Error t value Pr(>|t|)
(Intercept) 50.10072 0.31835002 157.3762 0.000000e+00
studyhours 1.48248 0.03043469 48.7102 2.579971e-210- Notice how the standard error for \(studyhours\) is smaller in the simple linear model. This is because it doesn’t account for the clustering, leading to an overestimation of the precision of the estimate.
Model Extensions and Considerations
- Random Slopes: Allow the effect of \(studyhours\) to vary across schools (not just the intercept). This is done by adding \((studyhours | school_id)\) to the \(lmer\) formula.
- Crossed Random Effects: When observations have multiple sources of clustering (e.g., students nested within schools AND neighborhoods).
- More Complex Models: Can include multiple predictors at both the individual and cluster levels.
- Model Selection: Use AIC, BIC, or likelihood ratio tests to compare different models (e.g., with and without random intercepts, with and without random slopes).
- Assumptions: Linearity, normality of residuals and random effects, independence of errors (within clusters, after accounting for the random effects), homoscedasticity. Check these assumptions using diagnostic plots.
- Software: \(lme4\) is the most common R package. Other options include \(nlme\), \(brms\) (for Bayesian mixed models), and \(glmmTMB\).
Sweet Spot For Bayesian Regression
- When you have a good prior knowledge about the parameters (e.g. from previous studies, expert opinion, etc.)
- When you want to quantify uncertainty in your estimates
- When you know that many of the predictors are not important (sparsity)
- When dealing with small sample sizes
- Hierarchical data (e.g. students within schools, patients within hospitals)
- Modeling nested relationships
- Sharing Information Across Groups
- When you want to compare multiple models
Examples where Bayesian Regression is Useful
- Medical Trials: Incorporating prior knowledge about treatment effects.
- Marketing: Predicting customer behavior with sparse data.
- Educational studies: Analyzing student performance within classrooms and schools, while accounting for variations in teacher effectiveness and school resources.
- Social sciences: Examining individual behavior within different communities or regions, while accounting for contextual factors and cultural differences.
- Ecology: Modeling species populations within different habitats or ecosystems, while considering environmental variations and species interactions
Bayesian Additive Regression Trees (BART)
Core Ideas of BART
- BART is a non-parametric Bayesian model used for both regression and classification.
- Its core idea is to represent a complex relationship between predictors (\(X\)) and a response variable (\(Y\)) as a sum of many simple regression trees.
- Each tree is a “weak learner.” It’s typically a small decision tree, often with only a - - Ensemble Power: The sum of the predictions from many of these weak learners creates a powerful and flexible model. This is similar in spirit to boosted trees (like XGBoost or LightGBM), but BART’s Bayesian nature provides important advantages.
The Model
\[ Y_i = f(X_i) + \epsilon_i f(X_i) = \sum_{j=1}^m g(X_i; T_j, M_j) \epsilon_i ~ N(0, \sigma^2) \]
Where:
- \(f(X_i)\) is the overall prediction function, which is the sum of the tree predictions.
- \(\epsilon_i\) is the error term, assumed to be normally distributed with mean 0 and variance \(\sigma^2\).
- \(m\) is the number of trees in the ensemble (a crucial hyperparameter).
- \(g(X_i; T_j, M_j)\) is the prediction from the j-th tree.
- \(T_j\) represents the tree structure (the splitting rules). It defines the splits based on the predictor variables and their values.
- \(M_j = {\mu_{1j}, \mu_{2j}, ..., \mu_{b_j j}}\) represents the set of terminal node parameters (the “leaf values”) for the j-th tree. \(b_j\) is the number of terminal nodes (leaves) in tree \(T_j\). Each leaf gets assigned a constant value (), which is the prediction for any observation that falls into that leaf.
Diagram
Code
graph TB
subgraph Input
X[Predictors]
end
subgraph BARTModel
Tree1((Tree 1)) --> Sum
Tree2((Tree 2)) --> Sum
TreeM((Tree M)) --> Sum
Sum[Sum of Trees]
end
subgraph Output
fX["f(X) - Prediction"]
end
Input --> BARTModel
BARTModel --> Output
fX --> Y["Y= f(X) + ε"]
Single Node
Example of a single tree (\(T_j\)):
Code
graph TD
A[X1 < 3] --> B{Yes};
A --> C{No};
B --> D[X2 > 7];
C --> E[X2 > 7];
D --> F("$$\mu_1$$");
D --> G("$$\mu2$$");
E --> H("$$\mu3$$");
E --> I("$$\mu4$$");
Bayesian Priors (The Bayesian Part)
- Prior on Tree Structure (\(T_j\)): prefer smaller trees: regularization and prevents overfitting. The prior for node splitting and choosing a particular predictor variable for splitting.
- Prior on Leaf Parameters (\(M_j\)): A common choice is a normal prior: \[ \mu_{kj} ~ N(0, \sigma_\mu^2) \] Prior 0: the trees are encouraged to make small “corrections” rather than large jumps.
- Prior on Error Variance (^2): An inverse-gamma prior is often used: \[
\sigma^2 ~ InverseGamma(\nu/2, \nu\lambda/2)
\]
- \(\nu\) (degrees of freedom) and \(\lambda\) (scale) are hyperparameters. This prior allows the model to learn the appropriate level of noise in the data.
Inference (MCMC)
- Because of the complex structure and the priors, we can’t directly calculate the posterior distribution of the parameters \((T_j, M_j, \sigma^2)\).
- Instead, BART uses Markov Chain Monte Carlo (MCMC) methods, specifically a Metropolis-within-Gibbs sampler, to draw samples from the posterior distribution.
The MCMC algorithm iteratively updates: \(T_j\) and \(M_j\)
Iterative Updates
- Each Tree (T_j and M_j): For each tree, the algorithm proposes changes to the tree structure (growing, pruning, changing splitting rules) and the leaf values. These proposals are accepted or rejected based on how well they improve the fit to the data, given the current state of all the other trees. This is the “backfitting” part of BART – each tree is adjusted to account for the predictions of the other trees.
- The Error Variance (^2): The error variance is updated based on the residuals (the difference between the observed \(Y\) values and the current model predictions).
The result of the MCMC process is a collection of samples from the posterior distribution of the model parameters.
Example in R (BART package)
Code
# Install the BART package if you haven't already
# install.packages("BART")
library(BART)
library(MASS) #For Boston Housing
# Load the Boston Housing dataset
data(Boston)
X <- Boston[, -14] # Predictors (all columns except 'medv')
Y <- Boston[, 14] # Response variable ('medv' - median house value)
# Fit the BART model
# - ntree: Number of trees (m in the formulas)
# - ndpost: Number of posterior samples to keep (after burn-in)
# - nskip: Number of burn-in iterations to discard
bart_model <- gbart(x.train = X, y.train = Y, ntree = 50, ndpost = 1000, nskip = 500)*****Calling gbart: type=1
*****Data:
data:n,p,np: 506, 13, 0
y1,yn: 1.467194, -10.632806
x1,x[n*p]: 0.006320, 7.880000
*****Number of Trees: 50
*****Number of Cut Points: 100 ... 100
*****burn,nd,thin: 500,1000,1
*****Prior:beta,alpha,tau,nu,lambda,offset: 2,0.95,1.59099,3,4.38629,22.5328
*****sigma: 4.745298
*****w (weights): 1.000000 ... 1.000000
*****Dirichlet:sparse,theta,omega,a,b,rho,augment: 0,0,1,0.5,1,13,0
*****printevery: 100
MCMC
done 0 (out of 1500)
done 100 (out of 1500)
done 200 (out of 1500)
done 300 (out of 1500)
done 400 (out of 1500)
done 500 (out of 1500)
done 600 (out of 1500)
done 700 (out of 1500)
done 800 (out of 1500)
done 900 (out of 1500)
done 1000 (out of 1500)
done 1100 (out of 1500)
done 1200 (out of 1500)
done 1300 (out of 1500)
done 1400 (out of 1500)
time: 2s
trcnt,tecnt: 1000,0Code
*****In main of C++ for bart prediction
tc (threadcount): 1
number of bart draws: 1000
number of trees in bart sum: 50
number of x columns: 13
from x,np,p: 13, 506
***using serial codeExample in R (BART package)
Code
# Plot predictions vs. actual values (with credible intervals)
plot(Y, mean_predictions, main = "BART Predictions vs. Actual Values",
xlab = "Actual Median House Value", ylab = "Predicted Median House Value",pch=16, cex=0.5)
segments(Y, credible_intervals[1, ], Y, credible_intervals[2, ], col = "gray")
abline(0, 1, col = "red") # Add a y=x line for reference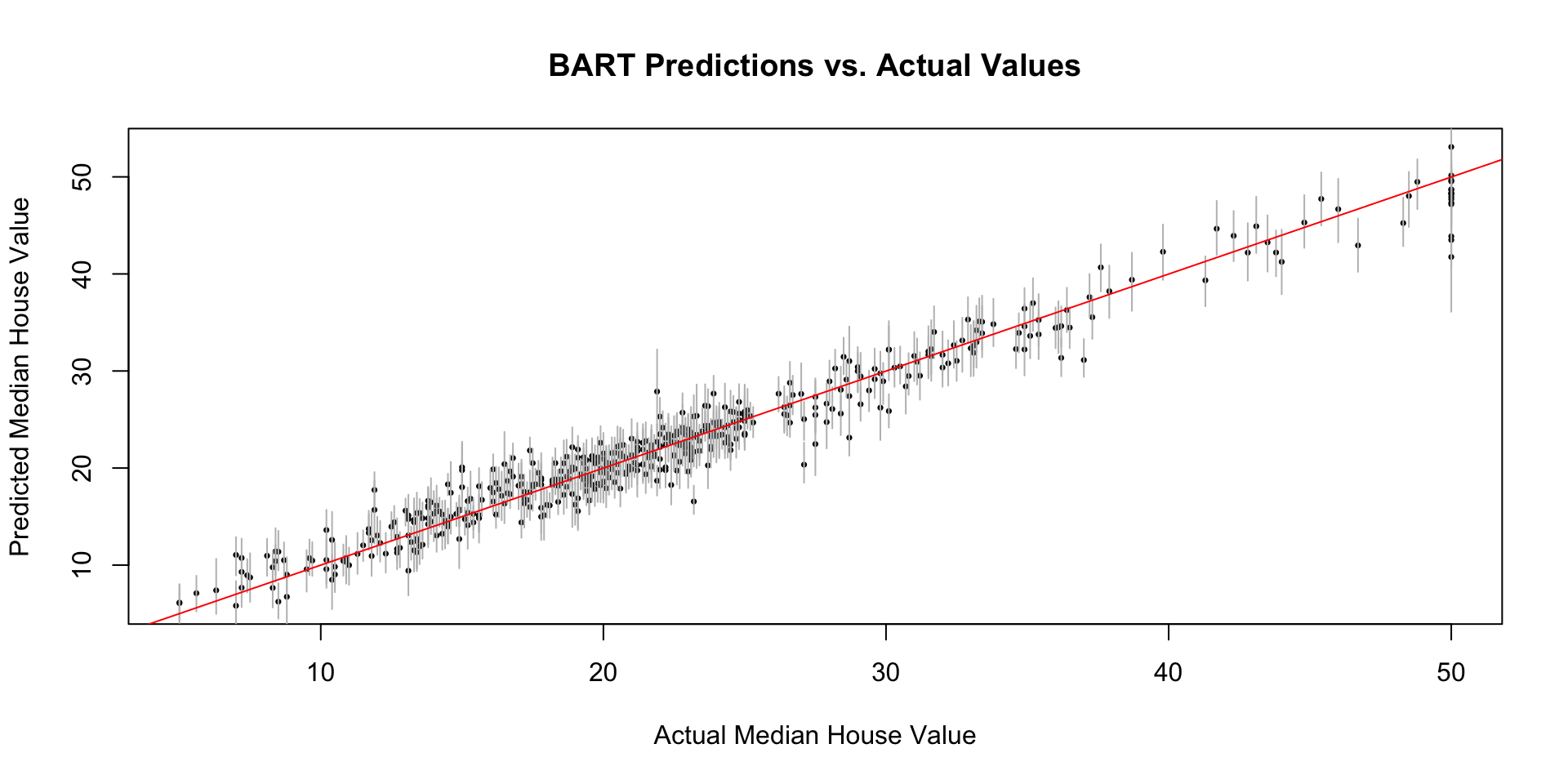
Example in R (BART package)
Example in R (BART package)
Example in R (BART package)
Code
*****In main of C++ for bart prediction
tc (threadcount): 1
number of bart draws: 1000
number of trees in bart sum: 50
number of x columns: 13
from x,np,p: 13, 5
***using serial codeCode
[1] 23.27826 21.08262 33.92599 33.88669 34.63011 [,1] [,2] [,3] [,4] [,5]
2.5% 20.57538 18.51734 31.90270 31.40777 32.50151
97.5% 25.87818 22.85859 35.95392 36.70508 36.66815Key Advantages of BART
- Flexibility: Can capture complex non-linear relationships and interactions between predictors.
- Regularization: The Bayesian priors and the sum-of-trees structure provide built-in regularization, reducing the risk of overfitting.
- Uncertainty Quantification: Provides credible intervals, giving a measure of uncertainty in the predictions.
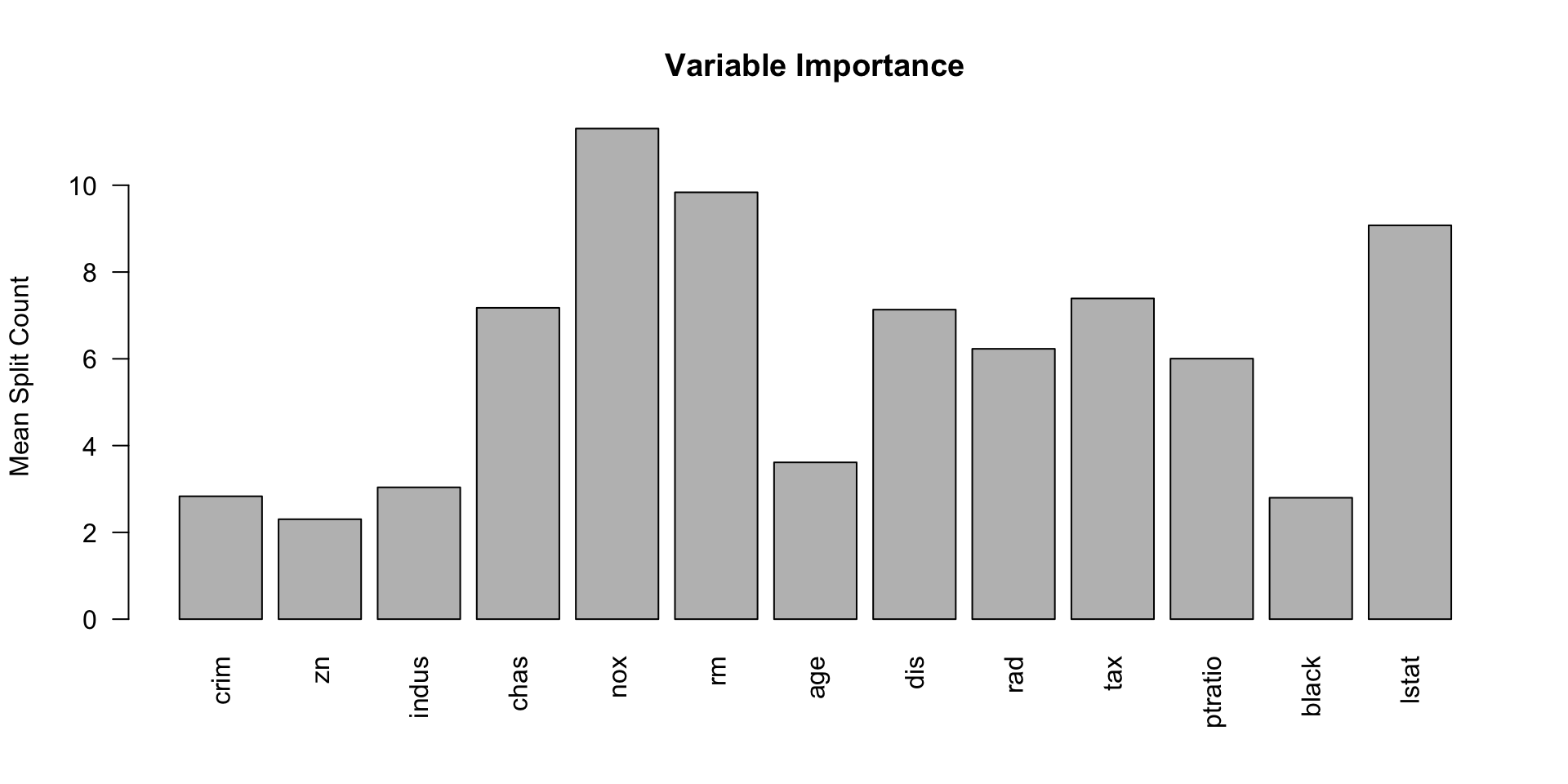
- Variable Importance: Provides a natural way to assess the importance of different predictors.
- Good Default Performance: Often performs well with minimal tuning of hyperparameters (although tuning can further improve performance).
Disadvantages and Considerations**
- Computational Cost: MCMC sampling can be computationally expensive, especially for large datasets and a large number of trees.
- Interpretability: While variable importance is helpful, the complex ensemble of trees can be difficult to interpret directly (compared to, say, a linear regression model). Partial dependence plots can help.
- Hyperparameter Tuning: While BART often works well with defaults, tuning \(ntree\), \(ndpost\), \(nskip\), and the prior parameters can further improve performance. Cross-validation is recommended for this. The \(BART\) package provides functions for this.
- Missing data: Handling missing data in BART could require imputation strategies before modelling.
MCMC Training Process
Code
graph LR
subgraph TrainingData
X_train[Training Predictors]
Y_train[Training Response]
end
subgraph BARTModel
Trees["Multiple Trees (Tj, Mj)"]
end
subgraph MCMC
MCMCIterations[MCMC Samples of Trees]
end
subgraph NewData
X_new[New Predictors]
end
subgraph Prediction
Predictions[Multiple Predictions]
MeanPrediction[Mean Prediction]
CredibleIntervals[Credible Intervals]
end
TrainingData --> BARTModel
BARTModel --> MCMCIterations
X_new --> MCMCIterations
MCMCIterations --> Predictions
Predictions --> MeanPrediction
Predictions --> CredibleIntervalsgraph LR
subgraph TrainingData
X_train[Training Predictors]
Y_train[Training Response]
end
subgraph BARTModel
Trees["Multiple Trees (Tj, Mj)"]
end
subgraph MCMC
MCMCIterations[MCMC Samples of Trees]
end
subgraph NewData
X_new[New Predictors]
end
subgraph Prediction
Predictions[Multiple Predictions]
MeanPrediction[Mean Prediction]
CredibleIntervals[Credible Intervals]
end
TrainingData --> BARTModel
BARTModel --> MCMCIterations
X_new --> MCMCIterations
MCMCIterations --> Predictions
Predictions --> MeanPrediction
Predictions --> CredibleIntervals
Temporal Data: Filtering, Event Detection, Pandemics
Example: History of Pandemics
Bill Gates: 12/11/2009: “I’m most worried about a worldwide Pandemic”
| Early-period Pandemics | Dates | Size of Mortality |
|---|---|---|
| Plague of Athens | 430 BC | 25% population. |
| Black Death | 1347 | 30% Europe |
| London Plague | 1666 2 | 0% population |
| Recent Flu Epidemics | Dates 1900-2010 | Size |
|---|---|---|
| Spanish Flu | 1918-19 40- | 50 million |
| Asian Flu | H2N2, 1957-58 2 | million |
| Hong Kong Flu | H3N2, 1968-69 6 | million |
Spanish Flu killed more than WW1
H1N1 Flu 2009: \(18,449\) people killed World wide:
SEIR Epidemic Models
Growth “self-reinforcing”: More likely if more infectants
An individual comes into contact with disease at rate \(\beta_1\)
The susceptible individual contracts the disease with probability \(\beta_2\)
Each infectant becomes infectious with rate \(\alpha\) per unit time
Each infectant recovers with rate \(\gamma\) per unit time
\(S_t + E_t + I_t + R_t = N\)
Current Models: SEIR
susceptible-exposed-infectious-recovered model
Dynamic models that extend earlier models to include exposure and recovery.
The coupled SEIR model:
\(\dot{S} = -\beta S I\)
\(\dot{E} = \beta S I - \alpha E\)
\(\dot{I} = \alpha E -\gamma I\)
\(\dot{R} = \gamma I\)
Infectious disease models
Daniel Bernoulli’s (1766) first model of disease transmission in smallpox:
“I wish simply that, in matters which so closely concern the well being of the human race, no decision shall be made without all knowledge which a little analysis and calculation can provide”
- R.A. Ross, (Nobel Medicine winner, 1902) – math model of malaria transmission, which ultimately lead to malaria control.
Ross-McDonald model
- Kermack and McKendrick: susceptible-infectious-recovered (SIR)
London Plague 1665-1666; Cholera: London 1865, Bombay, 1906.
Example: London Plague, 1666: Village Eyam nr. Sheffield
Model of transmission from Infectants, \(I\), to susceptibles, \(S\).
| Date 1666 Su | sceptibles In | fectives |
|---|---|---|
| Initial | 254 | 7 |
| July 3 | 235 15 | |
| July 19 | 201 22 | |
| Aug 3 1 | 53 29 | |
| Aug 19 | 121 21 | |
| Sept 3 | 108 8 | |
| Sept 19 | 97 8 | |
| Oct 3 | – | – |
| Oct 19 | 83 0 |
Initial Population \(N=261=S_0\); Final population \(S_\infty = 83\).
Modeling Growth: SI
Coupled Differential eqn \(\dot{S} = - \beta SI , \dot{I} = ( \beta S - \alpha ) I\)
- Estimates \(\frac{\beta}{\alpha} = 6.54 \times 10^{-3} , \frac{\alpha}{\beta} = 1.53\).
\[ \frac{ \hat{\beta} }{\alpha} = \frac{ \ln ( S_0 / S_\infty ) }{S_0 - S_\infty} \] Predicted maximum \(30.4\), very close to observed 29
Key: \(S\) and \(I\) are observed and \(\alpha , \beta\) are estimated in hindsight
Transmission Rates \(R_0\) for 1918 Episode
- 1918-19 influenza pandemic:
| Mills et al. 2004: | 45 US cities | 3 (2-4) |
| Viboud et al. 2006: | England and Wales | 1.8 |
| Massad et al. 2007: | Sao Paulo Brazil | 2.7 |
| Nishiura, 2007: | Prussia, Germany | 3.41 |
| Chowell et al., 2006: | Geneva, Switzerland | 2.7-3.8 |
| Chowell et al., 2007: | San Francisco | 2.7-3.5 |
The larger the \(R_0\) the more severe the epidemic.
Transmission parameters vary substantially from epidemic to epidemic
Boat Localization Example
Localization with measurement update
A boat sails from one island to another
Boat is trying to identify its location \(\theta \sim N(m_0, C_0)\)
Using a sequence of measurements to one of the islands \(x_1,\ldots,x_n\)
Measurements are noisy due to dilution of precision http://www.sailingmates.com/your-gps-can-kill-you/

Reckoning
Localization with no measurement updates is called reckoning

source: http://www.hakaimagazine.com/article-short/traversing-seas
Kalman Filter
\[
\theta \sim N(m_0, C_0)
\] \[
x_t = \theta + w_t,~~~w_t \sim N(0,\sigma^2)
\] \[
x_1,x_2,\ldots \mid \theta \sim N(\theta,\sigma^2)
\] The prior variance \(C_0\) might be quite large if you are very uncertain about your guess \(m_0\)
Given the measurements \(x^n = (x_1,\ldots,x_n)\), you update your opinion about \(\theta\) computing its posterior density, using the Bayes formula
Normal Model
\[ f(x) = \dfrac{1}{\sqrt{2 \pi \sigma^2}} \exp^{-\dfrac{1}{2}\dfrac{(x-\mu)^2}{\sigma^2}} \] Or multivariate equivalent \[ f(x) = (2 \pi)^{-k/2} |\Sigma|^{-1/2}\exp^{-0.5(x-\mu)^T\Sigma^{-1}(x-\mu)} \]
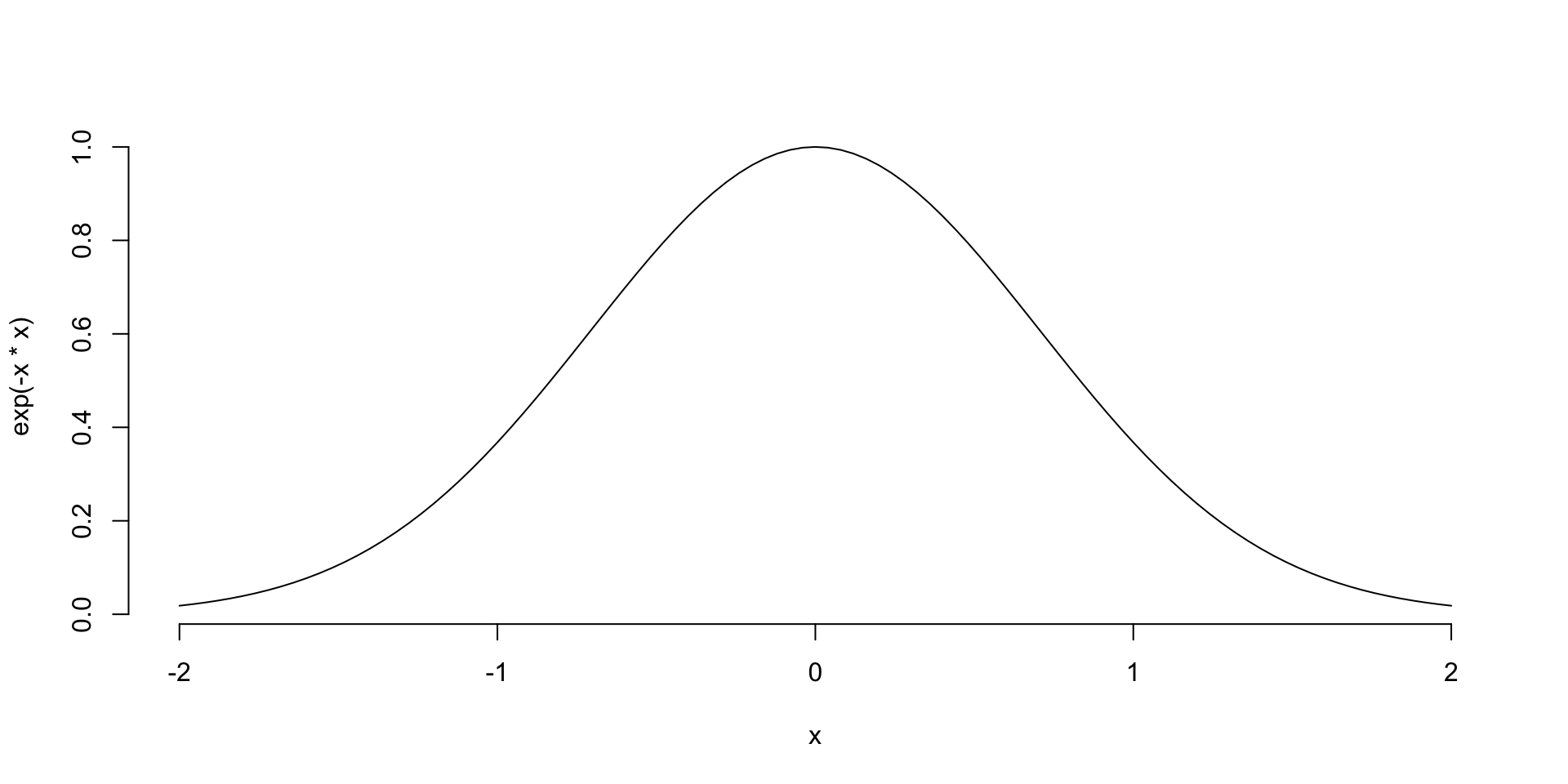
The Conjugate Prior for the Normal Distribution
We will look at the Gaussian distribution from a Bayesian point of view. In the standard form, the likelihood has two parameters, the mean \(\mu\) and the variance \(\sigma^2\) \[ p(x^n | \mu, \sigma^2) \propto \dfrac{1}{\sigma^n}\exp\left(-\dfrac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2\right) \]
Normal Prior
In case when we know the variance \(\sigma^2\), but do not know mean \(\mu\), we assume \(\mu\) is random. To have conjugate prior we choose \[ p(\mu | \mu_0, \sigma_0) \propto \dfrac{1}{\sigma_0}\exp\left(-\dfrac{1}{2\sigma_0^2}(\mu-\mu_0^2)\right) \] In practice, when little is known about \(\mu\), it is common to set the location hyper-parameter to zero and the scale to some large value.
Normal Model with Unknown Mean, Known Variance
Suppose we wish to estimate a model where the likelihood of the data is normal with an unknown mean \(\mu\) and a known variance \(\sigma^2\).
Our parameter of interest is \(\mu\). We can use a conjugate Normal prior on \(\mu\), with mean \(\mu_0\) and variance \(\sigma_0^2\). \[
\begin{aligned}
p(\mu| x^n, \sigma^2) & \propto p(x^n | \mu, \sigma^2)p(\mu) ~~~\mbox{(Bayes rule)}\\
N(\mu_1,\tau_1) & = N(\mu, \sigma^2)\times N(\mu_0, \sigma_0^2)
\end{aligned}
\]
Useful Identity
One of the most useful algebraic tricks for calculating posterior distribution is completing the square.
\[ \dfrac{(x-\mu_1)^2}{\sigma_1} + \dfrac{(x-\mu_2)^2}{\sigma_2} = \dfrac{(x - \mu_3)^2}{\sigma_3} + \dfrac{(\mu_1-\mu_2)^2}{\sigma_1 + \sigma_2} \] where \[ \mu_3 = \sigma_3 (\mu_1/\sigma_1 + \mu_2/\sigma_2) \] and \[ \sigma_3 = (1/\sigma_1 + 1/\sigma_2)^{-1} \]
Prior: \[ \theta \sim \frac{e^{-\frac{(\theta-\mu )^2}{2 \sigma ^2}}}{\sqrt{2 \pi } \sigma } \] Likelihood: \[ x \mid \theta \sim \frac{e^{-\frac{(\theta-y )^2}{2 r^2}}}{\sqrt{2 \pi } r} \] Posterior mean: \[ \frac{x \sigma ^2+\mu r^2}{r^2+\sigma ^2} \] Posterior variance: \[ \frac{1}{\frac{1}{r^2}+\frac{1}{\sigma ^2}} \]
Prior, Likelihood, Posterior
After \(n\) steps
\[ \begin{aligned} p(\mu | x^n) & \propto \prod_{i=1}^{n}\dfrac{1}{\sqrt{2\pi \sigma^2}}\exp\left(-\frac{(x_i - \mu )^2}{2\sigma^2}\right)\times\dfrac{1}{\sqrt{2\pi \sigma_0^2}}\exp\left(-\frac{(\mu - \mu_0)^2}{2\sigma_0^2}\right)\\ & \propto \exp\left(-\sum_{i=1}^{n}\frac{(x_i - \mu )^2}{2\sigma^2} - \frac{(\mu - \mu_0)^2}{2\sigma_0^2}\right)\\ & = \exp\left(-\dfrac{1}{2}\left[\sum_{i=1}^{n}\frac{(x_i - \mu )^2}{\sigma^2} + \frac{(\mu - \mu_0)^2}{\sigma_0^2}\right]\right)\\ & = \exp\left(-\dfrac{1}{2\sigma^2 \sigma_0^2}\left[\sigma_0^2\sum_{i=1}^{n}(x_i - \mu )^2 + \sigma^2 (\mu - \mu_0)^2\right]\right)\\ & = \exp\left(-\dfrac{1}{2\sigma^2 \sigma_0^2}\left[\sigma_0^2\sum_{i=1}^{n}(x_i^2 - 2\mu x_i+ \mu ^2) + \sigma^2 (\mu ^2 - 2\mu \mu_0 + \mu_0^2)\right]\right)\\\end{aligned} \]
After \(n\) steps
We can multiply the \(2\mu x_i\) term in the summation by \(n/n\) in order to get the equations in terms of the sufficient statistic \(\bar{x}^n\) \[ \begin{aligned} p(\mu | x^n) & \propto \exp\left(-\dfrac{1}{2\sigma^2 \sigma_0^2}\left[\sigma_0^2\sum_{i=1}^{n}(x_i^2 - \dfrac{n}{n}2\mu x_i+ \mu ^2) + \sigma^2 (\mu ^2 - 2\mu \mu_0 + \mu_0^2)\right]\right)\\ & = \exp\left(-\dfrac{1}{2\sigma^2 \sigma_0^2}\left[\sigma_0^2\sum_{i=1}^{n}x_i^2 - \sigma_0^22\mu n\bar{x}^n+ \tau_n^0n\mu ^2 + \sigma^2 \mu ^2 - 2\mu \mu_0\sigma^2 + \mu_0^2\sigma^2\right]\right)\end{aligned} \] set \(k = \sigma_0^2\sum_{i=1}^{n}x_i^2 + \mu_0^2\sigma^2\) (they do not contain \(\mu\)) \[ p(\mu | x^n) \propto \exp\left(-\dfrac{1}{2}\left[\mu ^2\left(\dfrac{1}{\sigma_0^2} + \dfrac{n}{\sigma^2}\right) - 2\mu\left(\dfrac{\mu_0}{\sigma_0^2} + \dfrac{n\bar{x}^n}{\sigma^2}\right) + k\right]\right) \]
After \(n\) steps
Let’s multiply by \[ \dfrac{1/\sigma_0^2 + n/\sigma^2}{1/\sigma_0^2 + n/\sigma^2} \] Now \[ p(\mu | x^n) \propto \exp\left(-\dfrac{1}{2}\left(1/\sigma_0^2 + n/\sigma^2\right)\left(\mu - \dfrac{\mu_0/\sigma_0^2 + n\bar{x}^n/\sigma^2}{1/\sigma_0^2 + n/\sigma^2}\right)^2\right) \]
\[ p(\mu | x^n) \propto \exp\left(-\dfrac{1}{2}\left(1/\sigma_0^2 + n/\sigma^2\right)\left(\mu - \dfrac{\mu_0/\sigma_0^2 + n\bar{x}^n/\sigma^2}{1/\sigma_0^2 + n/\sigma^2}\right)^2\right) \]
After \(n\) steps
Posterior mean: \(\mu_n = \dfrac{\mu_0/\sigma_0^2 + n\bar{x}^n/\sigma^2}{1/\sigma_0^2 + n/\sigma^2}\)
Posterior variance: \(\sigma_n^2 = \left(1/\sigma_0^2 + n/\sigma^2\right)^{-1}\)
Posterior precision:: \(\tau_n^2 = 1/\sigma_0^2 + n/\sigma^2\)
Posterior Precision is just the sum of the prior precision and the data precision.
Posterior Mean
\[ \begin{aligned} \mu_n & = \dfrac{\mu_0/\sigma_0^2 + n\bar{x}^n/\sigma^2}{1/\sigma_0^2 + n/\sigma^2}\\ & = \dfrac{\mu_0\sigma^2}{\sigma^2 + n\sigma_0^2} + \dfrac{\sigma_0^2n\bar{x}^n}{\sigma^2 + n\sigma_0^2}\end{aligned} \]
As \(n\) increases, data mean dominates prior mean.
As \(\sigma_0^2\) decreases (less prior variance, greater prior precision), our prior mean becomes more important.
A state space model
A state space model consists of two equations: \[ \begin{aligned} Z_t&=HS_t+w_t\\ S_{t+1} &= FS_t + v_t\end{aligned} \] where \(S_t\) is a state vector of dimension \(m\), \(Z_t\) is the observed time series, \(F\), \(G\), \(H\) are matrices of parameters, \(\{w_t\}\) and \(\{v_t\}\) are \(iid\) random vectors satisfying \[ \mbox{E}(w_t)=0, \hspace{0.5cm} \mbox{E}(v_t)=0, \hspace{0.5cm}\mathrm{cov}(v_t)=V, \hspace{0.5cm} \mathrm{cov}(w_t)=W \] and \(\{w_t\}\) and \(\{v_t\}\) are independent.
State Space Models
State space models consider a time series as the output of a dynamic system perturbed by random disturbances.
Natural interpretation of a time series as the combination of several components, such as trend, seasonal or regressive components.
Computations can be implemented by recursive algorithms.
Types of Inference
Model building versus inferring unknown variable. Assume a linear model \(Z = HS + \epsilon\)
Model building: know signal \(S\), observe \(Z\), infer \(H\) (a.k.a. model identification, learning)
Estimation: know \(H\), observe \(Z\), estimate \(S\)
Hypothesis testing: unknown takes one of few possible values; aim at small probability of incorrect decision
Estimation: aim at a small estimation error
Time Series Estimation Tasks
Filtering: To recover the state vector \(S_t\) given \(Z^t\)
Prediction: To predict \(S_{t+h}\) or \(Z_{t+h}\) for \(h > 0\), given \(Z^t\)
Smoothing: To estimate \(S_t\) given \(Z^T\) , where \(T > t\)
Property of Multivariate Normal
Under normality, we have
that normal prior plus normal likelihood results in a normal posterior,
that if the random vector \((X, Y )\) are jointly normal
\[ \begin{bmatrix} X\\ Y \end{bmatrix} \sim N\left( \begin{bmatrix} \mu_x\\ \mu_y \end{bmatrix}, \begin{bmatrix} \Sigma_{xx}&\Sigma_{xy}\\ \Sigma_{yx}&\Sigma_{yy}\\ \end{bmatrix}\right), \]
- then the conditional distribution of \(X\) given \(Y = y\) is normal
\[ X|Y = y\sim N\left[\mu_x+\Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y),\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}\right]. \]
From State Space Model
\[ \begin{aligned} S_{t+1}^t &= FS_t\\ Z_{t+1}^t &=HS_{t+1}^t\\ P_{t+1}^t&=FP_tF^T+GQG^T\\ V_{t+1}^t&=HP_{t+1}^tH^T+R\\ C_{t+1}^t&=HP_{t+1}^t \end{aligned} \]
\(P_{t+j}^t\) = conditional covariance matrix of \(S_{t+j}\) given \(\{Z_t , Z_{t-1} , \cdots\}\) for \(j \geq 0\)
\(S_{t+j}^t\) = conditional mean of \(S_{t+j}\) given \(\{Z_t , Z_{t-1} , \cdots\}\)
\(V_{t+1}^t\) = conditional variance of \(Z_{t+1}\) given \(Z^t = \{Z_t , Z_{t-1} , \cdots\}\)
\(C_{t+1}^t\) = conditional covariance between \(Z_{t+1}\) and \(S_{t+1}\)
Joint conditional distribution \(P(S_{t+1}, Z_{t+1} | Z^t)\)
\[ \begin{bmatrix} S_{t+1}\\ Z_{t+1} \end{bmatrix}_t \sim N \left( \begin{bmatrix} S_{t+1}^t\\ Z_{t+1}^t \end{bmatrix}, \begin{bmatrix} P_{t+1}^t & P_{t+1}^tH'\\ HP_{t+1}^t & HP_{t+1}^tH'+R \end{bmatrix} \right) \]
\(P(S_{t+1}| Z_{t+1})\)
Finally, when \(Z_{t+1}\) becomes available, we may use the property of nromality to update the distribution of \(S_{t+1}\) . More specifically, \[ S_{t+1}=S_{t+1}^t+P_{t+1}^tH^T[HP_{t+1}^tH^T+R]^{-1}(Z_{t+1}-Z_{t+1}^t) \] and \[ P_{t+1}=P_{t+1}^t-P_{t+1}^tH^T[HP_{t+1}^tH'+R]^{-1}HP_{t+1}^t. \] Predictive residual: \[ R_{t+1}^t=Z_{t+1}-Z_{t+1}^t=Z_{t+1}-HS_{t+1}^t \ne 0 \] means there is new information about the system so that the state vector should be modified. The contribution of \(r_{t+1}^t\) to the state vector, of course, needs to be weighted by the variance of \(r_{t+1}^t\) and the conditional covariance matrix of \(S_{t+1}\).
Kalman filter
Predict: \[ \begin{aligned} S_{t+1}^t &= FS_t\\ Z_{t+1}^t &=HS_{t+1}^t\\ P_{t+1}^t&=FP_tF^T+GQG^T\\ V_{t+1}^t&=HP_{t+1}^tH^T+R \end{aligned} \]
Update: \[ \begin{aligned} S_{t+1|t+1}=& S_{t+1}^t+P_{t+1}^tH^T[HP_{t+1}^tH^T+R]^{-1}(Z_{t+1}-Z_{t+1}^t)\\ P_{t+1|t+1}=& P_{t+1}^t-P_{t+1}^tH^T[HP_{t+1}^tH^T+R]^{-1}HP_{t+1}^t \end{aligned} \]
Kalman filter
starts with initial prior information \(S_{0}\) and \(P_{0}\)
predicts \(Z_{1}^0\) and \(V_{1}^0\)
Once the observation \(Z_1\) is available, uses the updating equations to compute \(S_{1}\) and \(P_{1}\)
\(S_{1|1}\) and \(P_{1|1}\) is the prior for the next observation.
This is the Kalman recusion.
Kalman filter
effect of the initial values \(S_{0}\) and \(P_{0}\) is decresing as \(t\) increases
for a stationary time series, all eigenvalues of the coefficient matrix \(F\) are less than one in modulus
Kalman filter recursion ensures that the effect of the initial values indeed vanishes as \(t\) increases
uncertainty about the state is always normal
Local Trend Model
\[ \begin{aligned} y_t =& \mu_t + e_t,~e_t \sim N(0,\sigma_e^2)\\\ \mu_{t+1} =& \mu_t + \eta_t,~ \eta_t \sim N(0,\sigma_{\eta}^2 ) \end{aligned} \]
\(\{e_t\}\) and \(\{\eta_t\}\) are iid Gaussian white noise
\(\mu_0\) is given (possible as a distributed value)
trend \(\mu_t\) is not observable
we observe some noisy version of the trend \(y_t\)
such a model can be used to analyze realized volatility: \(\mu_t\) is the log volatility and \(y_t\) is constructed from high frequency transactions data
Local Trend Model
\[ \begin{aligned} y_t =& \mu_t + e_t,~e_t \sim N(0,\sigma_e^2)\\\ \mu_{t+1} =& \mu_t + \eta_t,~ \eta_t \sim N(0,\sigma_{\eta}^2 ) \end{aligned} \]
if \(\sigma_e=0\), then we have ARIMA(0,1,0) model
if \(\sigma_e > 0\), then we have ARIMA(0,1,1) model, satisfying
\[ (1-B)y_t = (1-\theta B)a_t, ~ a_t \sim N(0,\sigma_a^2) \] \(\sigma_a\) and \(\theta\) are determined by \(\sigma_e\) and \(\sigma_{\eta}\) \[ (1-B)y_t = \eta_{t-1} + e_t - e_{t-1} \]
Liner Regression (time dependent parameters)
\[ \begin{aligned} y_t &= \alpha_t + \beta_t \, x_t + \epsilon_t \qquad & \epsilon_t \, \sim N(0,\sigma^2) \\ \alpha_t &= \quad \alpha_{t-1} + \epsilon_t^{\alpha} \qquad & \epsilon_t^{\alpha} \sim N(0,\sigma_{\alpha}^2) \\ \beta_t &= \quad \beta_{t-1} + \epsilon_t^{\beta} \qquad & \epsilon_t^{\beta} \sim N(0, \sigma_{\beta}^2) \\ \end{aligned} \]
dlm Package
dlmModARMA: for an ARMA process, potentially multivariatedlmModPoly: for an \(n^{th}\) order polynomialdlmModReg: for Linear regressiondlmModSeas: for periodic – Seasonal factorsdlmModTrig:for periodic – Trigonometric form
Local Linear Trend
\[ \begin{aligned} y_t &= \qquad \quad \mu_t + \upsilon_t \quad &\upsilon_t \sim N(0,V) \\ \mu_t &= \mu_{t-1} + \delta_{t-1} + \omega_t^{\mu} \quad & \omega_t^{\mu} \sim N(0,W^{\mu}) \\ \delta_t &= \qquad \,\, \, \delta_{t-1} + \omega_t^{\delta} \quad & \omega_t^{\delta} \sim N(0,W^{\delta}) \\ \end{aligned} \]
Simple exponential smoothing with additive errors
\[ x_t = \ell_{t-1} + \varepsilon_t \] \[ \ell_t=\ell_{t-1}+\alpha \varepsilon_t. \]
Holt’s linear method with additive errors
\[ \begin{aligned} y_t&=\ell_{t-1}+b_{t-1}+\varepsilon_t\\ \ell_t&=\ell_{t-1}+b_{t-1}+\alpha \varepsilon_t\\ b_t&=b_{t-1}+\beta \varepsilon_t, \end{aligned} \]
Relation to ARMA models
Consider relation with ARMA models. The basic relations are
an ARMA model can be put into a state space form in “infinite" many ways;
for a given state space model in, there is an ARMA model.
State space model to ARMA model
The second possibility is that there is an observational noise. Then, the same argument gives \[ (1+\alpha_1B+\cdots+\alpha_mB^m)(Z_{t+m}-\epsilon_{t+m})=(1-\theta_1B-\cdots -\theta_{m-1}B^{m-1})a_{t+m} \] By combining \(\epsilon_t\) with \(a_t\) , the above equation is an ARMA\((m, m)\) model.
ARMA model to state space model: AR(2)
\[ Z_t=\phi_1Z_{t-1}+\phi_2Z_{t-2}+a_t \] For such an AR(2) process, to compute the forecasts, we need \(Z_{t-1}\) and \(Z_{t-2}\) . Therefore, it is easily seen that \[ \begin{bmatrix} Z_{t+1}\\ Z_t \end{bmatrix} = \begin{bmatrix} \phi_1 & \phi_2\\ 1 & 0 \end{bmatrix} \begin{bmatrix} Z_t\\ Z_{t-1} \end{bmatrix} + \begin{bmatrix} 1\\ 0 \end{bmatrix} e_t, \] where \(e_t = a_{t+1}\) and \[ Z_t=[1, 0]S_t \] where \(S_t = (Z_t , Z_{t-1})^T\) and there is no observational noise.
ARMA model to state space model: MA(2)
\[
Z_t=a_t-\theta_1a_{t-1}-\theta_2a_{t-2}
\] Method 1:
\[
\begin{bmatrix}
a_t\\
a_{t-1}
\end{bmatrix}
=
\begin{bmatrix}
0 & 0\\
1 & 0
\end{bmatrix}
\begin{bmatrix}
a_{t-1}\\
a_{t-2}
\end{bmatrix}
+
\begin{bmatrix}
1\\
0
\end{bmatrix}
a_t
\]
\[
Z_t=[-\theta_1, -\theta_2]S_{t-1} + a_t
\] Here the innovation \(a_t\) shows up in both the state transition equation and the observation equation. The state vector is of dimension 2.
ARMA model to state space model: MA(2)
Method 2: For an MA(2) model, we have \[ \begin{aligned} Z_{t}^t&=Z_t\\ Z_{t+1}^t&=-\theta_1a_t-\theta_2a_{t-1}\\ Z_{t+2}^t&= -\theta_2a_t \end{aligned} \] Let \(S_t = (Z_t , -\theta_1 a_t - \theta_2 a_{t-1} , -\theta_2 a_t )^T\) . Then, \[ S_{t+1}= \begin{bmatrix} 0 & 1& 0\\ 0& 0& 1\\ 0& 0& 0 \end{bmatrix} S_t+ \begin{bmatrix} 1\\ -\theta_1\\ -\theta_2 \end{bmatrix} a_{t+1} \] and \[ Z_t=[1,0,0]S_t \] Here the state vector is of dimension 3, but there is no observational noise.
ARMA model to state space model: Akaike’s approach
Consider ARMA\((p, q)\) process, let \(m = max\{p, q + 1\}\), \(\phi_i = 0\) for \(i > p\) and \(\theta_j = 0\) for \(j > q\). \[ S_t = (Z_t , Z_{t+1}^t , Z_{t+2}^t ,\cdots , Z_{t+m-1}^t )^T \] where \(Z_{t+\ell}^t\) is the conditional expectation of \(Z_{t+\ell}\) given \(\Psi_t = \{Z_t , Z_{t-1} , \cdots\}\). By using the updating equation \(f\) forecasts (recall what we discussed before) \[ Z_{t+1}(\ell -1)=Z_t(\ell)+\psi_{\ell-1}a_{t+1}, \]
ARMA model to state space model: Akaike’s approach
\[ S_t = (Z_t , Z_{t+1}^t , Z_{t+2}^t ,\cdots , Z_{t+m-1}^t )^T \] \[ S_{t+1}=FS_t+Ga_{t+1} \]
\[ Z_t=[1,0, \cdots ,0]S_t \] where \[ F= \left[ \begin{array}{c|cccc} 0 &1& 0& \cdots& 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & & \\ \phi_m & \phi_{m-1} & \cdots & \phi_2 & \phi_1 \end{array}\right], G= \begin{bmatrix} 1\\ \psi_1\\ \psi_2\\ \vdots\\ \psi_{m-1} \end{bmatrix} \] The matrix \(F\) is call a companion matrix of the polynomial \(1 - \phi_1 B - \cdots - \phi_m B^m\).
ARMA model to state space model: Aoki’s Method
Two-step procedure: First, consider the MA\((q)\) part: \[ W_t = a_t - \theta_1 a_{t-1} - \cdots - \theta_q a_{t-q} \] \[ \begin{bmatrix} a_t\\ a_{t-1}\\ \vdots\\ a_{t-q+1} \end{bmatrix} = \begin{bmatrix} 0&0&\cdots & 0&0\\ 1&0& \cdots&0&0\\ \vdots & & & &\\ 0 & 0 & \cdots & 1 & 0 \end{bmatrix} \begin{bmatrix} a_{t-1}\\ a_{t-2}\\ \vdots\\ a_{t-q} \end{bmatrix} + \begin{bmatrix} 1\\ 0\\ \vdots\\ 0 \end{bmatrix} a_t \]
\[ W_t=[-\theta_1,-\theta_2, \cdots, -\theta_q]S_t+a_t \]
ARMA model to state space model: Aoki’s Method
First, consider the AR\((p)\) part: \[ Z_t = \phi_1 Z_{t-1} + ... + \phi_p Z_{t-p} + W_t \] Define state-space vector as \[ S_t=(Z_{t-1},Z_{t-2}, \cdots , Z_{t-p},a_{t-1}, \cdots, a_{t-q})' \] Then, we have \[ \begin{bmatrix} Z-t\\ Z_{t-1}\\ \vdots\\ Z_{t-p+1}\\ a_t\\ a_{t-1}\\ \vdots\\ a_{t-q+1} \end{bmatrix} = \left[ \begin{array}{cccc|cccc} \phi_1&\phi_2&\cdots&\phi_p&-\theta_1&-\theta_2&\cdots&-\theta_q\\ 1&0&\cdots&0&0&0&\cdots&0\\ \vdots &&&&\vdots&&&\\ 0&\cdots&1&0&0&0&\cdots&0\\ 0&0&\cdots&0&0&0&\cdots&0\\ 0&0&\cdots&0&1&0&\cdots&0\\ \vdots &&&&0&&&\\ 0&0&\cdots&0&0&\cdots&1&0 \end{array}\right] \begin{bmatrix} Z_{t-1}\\ Z_{t-2}\\ \vdots\\ Z_{t-p}\\ a_{t-1}\\ a_{t-2}\\ \vdots\\ a_{t-q} \end{bmatrix}+ \begin{bmatrix} 1\\ 0\\ \vdots\\ 0\\ 1\\ 0\\ \vdots\\ 0 \end{bmatrix}a_t \] and \[ Z_t=[\phi_1,\cdots,\phi_p,-\theta_1,\cdots,-\theta_q]S_t+a_t \]
MLE Estimation
Innovations are given by \[ \epsilon_t = Z_t - HS_t^{t-1} \] can be shown that \(\mathrm{var}(\epsilon_t) = \Sigma_t\), where \[ \Sigma_t = HP_t^{t-1}H^T + R \] Incomplete Data Likelihood: \[ -\ln L(\Theta) = \dfrac{1}{2}\sum_{t=1}^{n}\log|\Sigma_t(\Theta)| + \dfrac{1}{2}\sum_{t=1}^{n}\epsilon_t(\Theta)^T\Sigma(\Theta)^{-1}\epsilon_t(\Theta) \] Here \(\Theta = (F, Q, R)\). Use BFGS to find a sequence of \(\Theta\)’s and stop when stagnation happens.
Kalman Smoother
Input: initial distribution \(X_0\) and data \(Z_1,...,Z_T\)
Algorithm: forward-backward pass
Forward pass: Kalman filter: compute \(S_{t+1}^t\) and \(S_{t+1}^{t+1}\) for \(0 \le t < T\)
Backward pass: Compute \(S_t^T\) for \(0 \le t < T\)
Backward Pass
Compute \(X_t^T\) given \(S_{t+1}^T \sim N(m_{t+1}^T,C_{t+1}^T)\)
Reverse arrow: \(S_t^t \leftarrow X_{t+1}^t\)
Same as incorporating measurement in filter
Compute joint \((S_t^t, S_{t+1}^t)\)
Compute conditional \((S_t^t \mid S_{t+1}^t )\)
New: \(S_{t+1}\) is not “known”, we only know its distribution: \(S_{t+1} \sim S_{t+1}^T\)
“Uncondition” on \(S_{t+1}\) to compute \(S_t^T\) using laws of total expectation and variance
Kalman Smoother
A smoothed version of data (an estimate, based on the entire data set) If \(S_n\) and \(P_n\) obtained via Kalman recursions, then for \(t=n,..,1\) \[ \begin{aligned} S_{t-1}^t &= S_{t-1} + J_{t-1}(S_t^n - S_t^{t-1})\\ P_{t-1}^n &= P^{t-1} + J_{t-1}(P_t^n - P_t^{t-1})J^T_{t-1}\\ J_{t-1} & = P_{t-1}F^T[P_t^{t-1}]^{-1} \end{aligned} \]
Kalman and Histogran Filter Shortciomings
Kalman:
linear dynamics
linear measurement model
normal errors
unimodal uncertainty
Histogram:
discrete states
approximation
inefficient in memory
MCMC Financial Econometrics
Set of tools for inference and pricing in continuous-time models.
Simulation-based and provides a unified approach to state and parameter inference. Can also be applied sequentially.
Can handle Estimation and Model risk. Important implications for financial decision making
Bayesian inference. Uses conditional probability to solve an inverse problem and estimates expectations using Monte Carlo.
Filtering, Smoothing, Learning and Prediction
Data \(y_{t}\) depends on a , \(x_{t}\). \[ \begin{aligned} \text{Observation equation} & \text{:\ }y_{t}=f\left( x_{t},\varepsilon _{t}^{y}\right) \\ \text{State evolution} & \text{: }x_{t+1}=g\left( x_{t},\varepsilon _{t+1}^{x}\right) ,\end{aligned} \]
Posterior distribution of \(p\left(x_{t}|y^{t}\right)\) where \(y^{t}=\left( y_{1},...,y_{t}\right)\)
Prediction and Bayesian updating.
\[ p\left( x_{t+1}|y^{t}\right) =\int p\left( x_{t+1}|x_{t}\right) p\left( x_{t}|y^{t}\right) dx_{t},\label{Predict}% \] updated by Bayes rule
\[ \underset{\text{Posterior}}{\underbrace{p\left( x_{t+1}|y^{t+1}\right) }% }\propto\underset{\text{Likelihood}}{\underbrace{p\left( y_{t+1}% |x_{t+1}\right) }}\underset{\text{Prior}}{\underbrace{p\left( x_{t+1}% |y^{t}\right) }}.\label{Update}% \]
Nonlinear Model
The observation and evolution dynamics are \[ \begin{aligned} y_t & = \frac{x_t}{1+ x_t^2} + v_t \; , {\rm where} \; v_t \sim N(0,1) \\ x_t & = x_{t-1} + w_t \; , {\rm where} \; w_t \sim N(0,0.5)\end{aligned} \]
Initial condition \(x_0 \sim N( 1 , 10 )\)
Fundamental question:
How do the filtering distributions \(p(x_t|y^t)\) propagate in time?
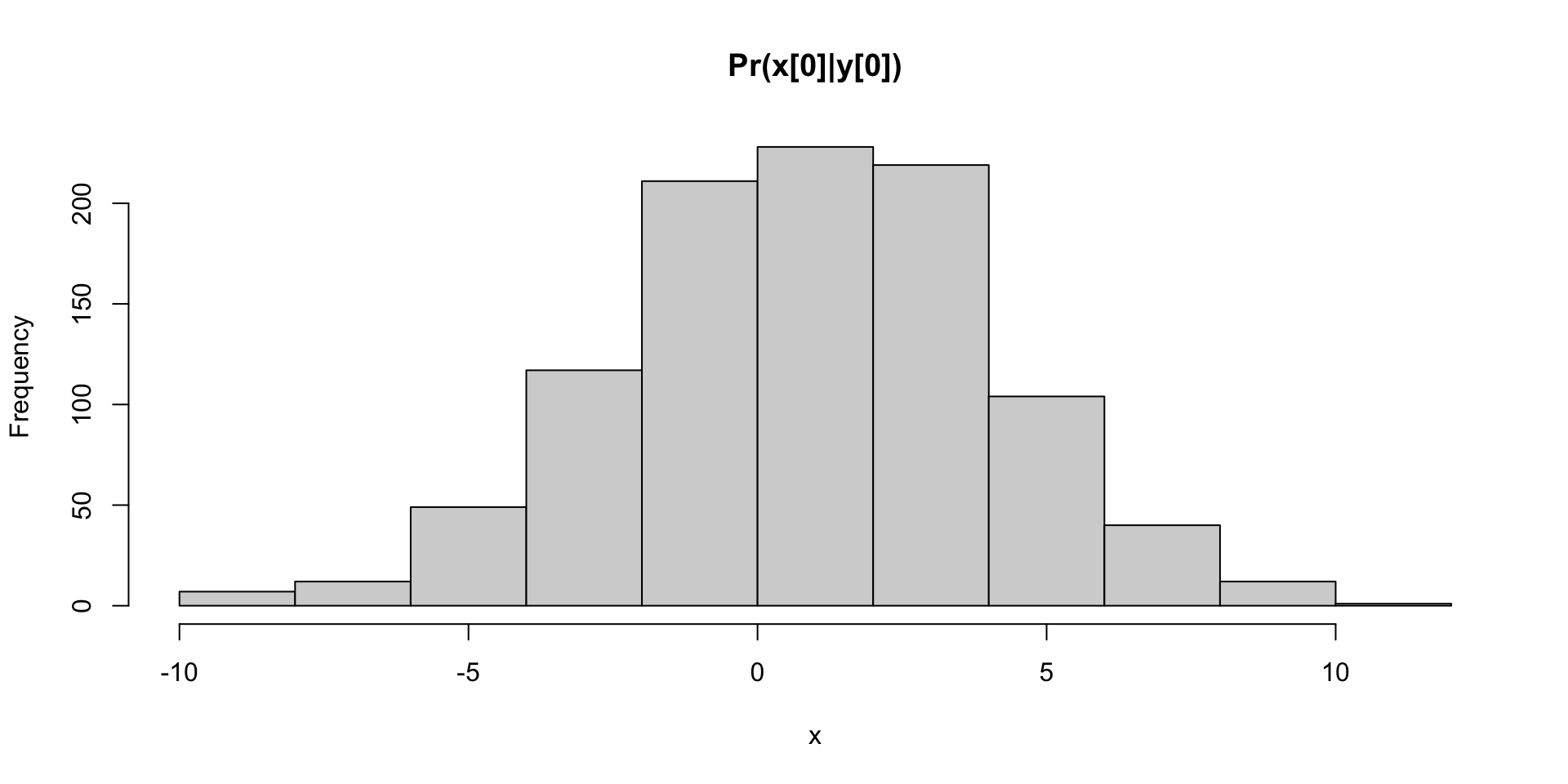
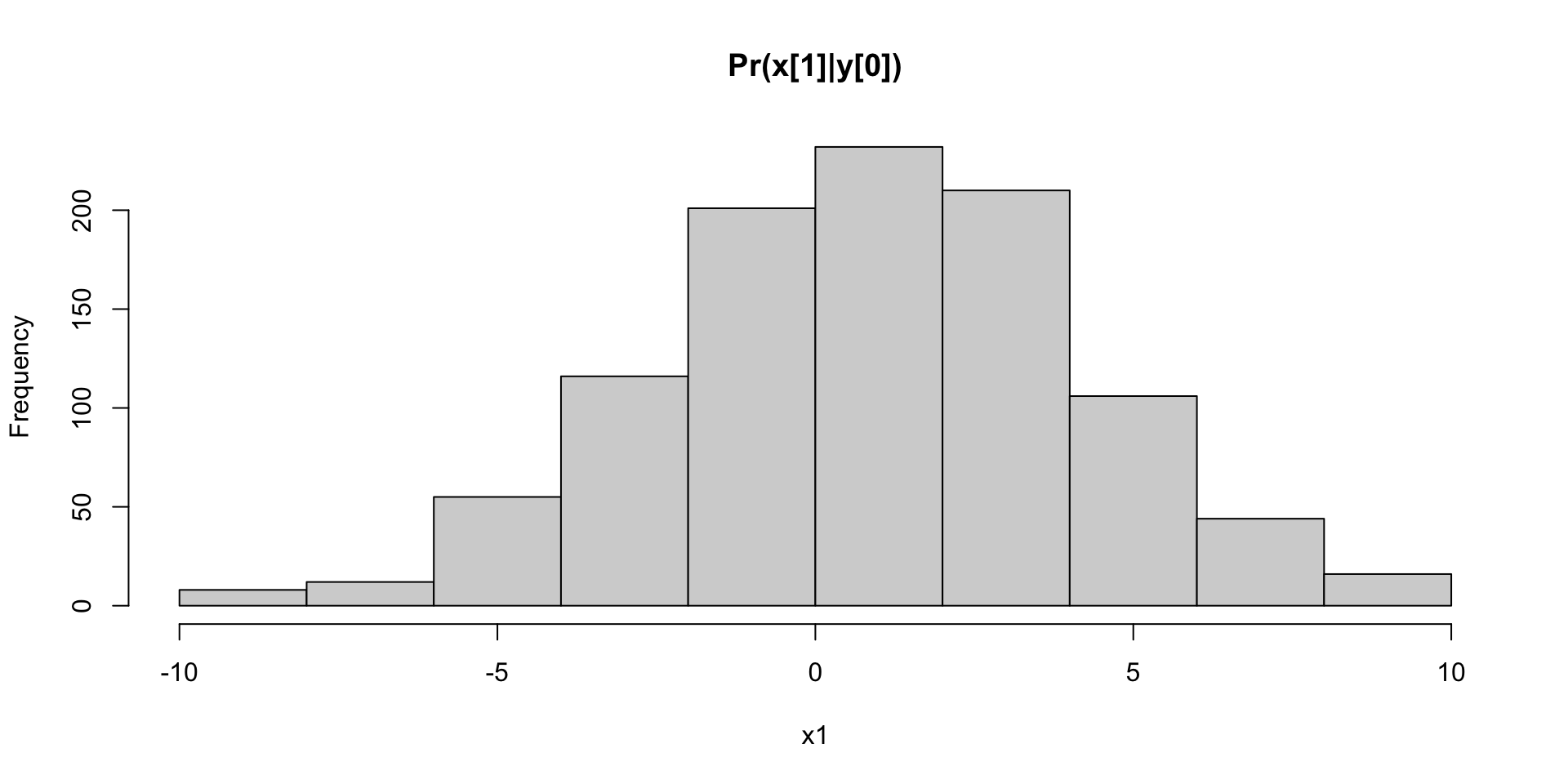
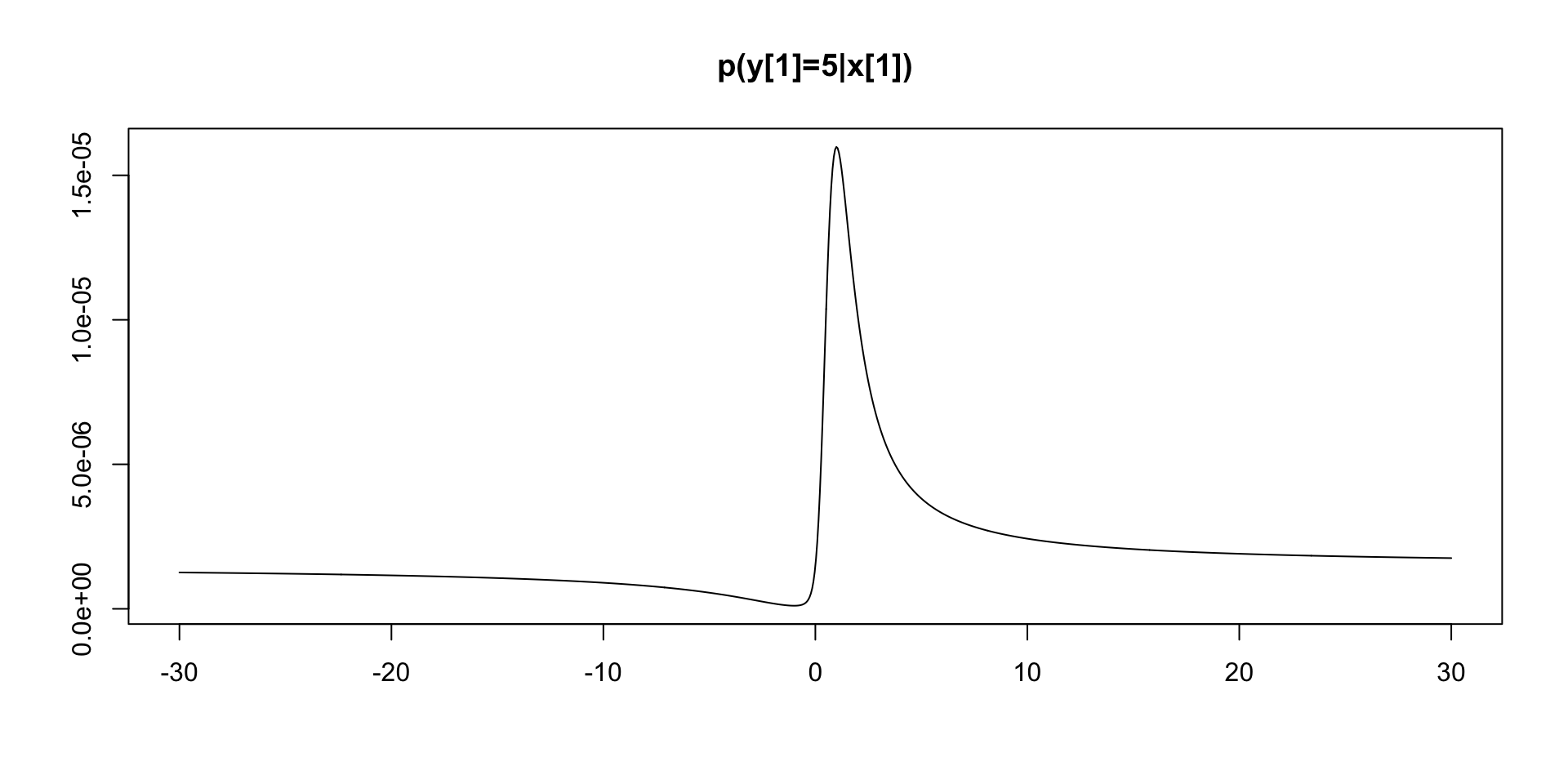
Nonlinear: \(y_t = x_t / (1+ x_t^2) + v_t\)
Simulate Data
Code
Code
Code
Nonlinear Filtering
Resampling
Key: resample and propagate particles
Propagation of MC error
Dynamic Linear Model (DLM): Kalman Filter
Kalman filter for linear Gaussian systems
- FFBS (Filter Forward Backwards Sample)
This determines the posterior distribution of the states
\[ p( x_t | y^t ) \; {\rm and} \; p( x_t | y^T ) \] Also the joint distribution \(p( x^T | y^T )\) of the hidden states.
Discrete Hidden Markov Model HMM (Baum-Welch, Viterbi)
With parameters known the Kalman filter gives the exact recursions.
Simulate DLM
Dynamic Linear Models \[ y_t = x_t + v_t \; \; {\rm and} \; \; x_t = \alpha + \beta x_{t-1} + w_t \] Simulate Data
Exact calculations
Kalman Filter recursions
DLM Data
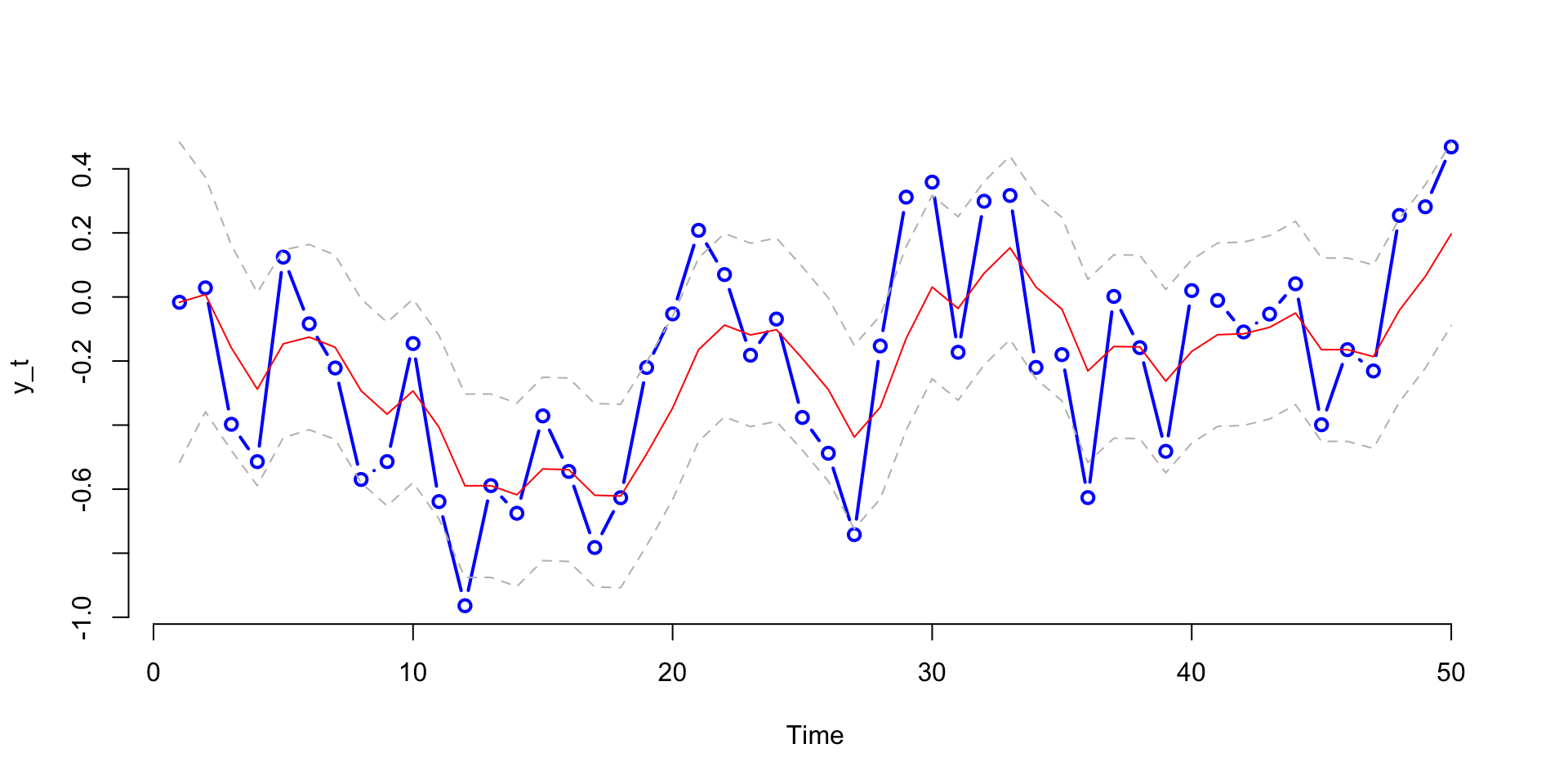
Bootstrap Filter
Code
M = 1000
h = rnorm(M,m0,sqrt(C0))
hs = NULL
for (t in 1:T1){
h1 = rnorm(M,alpha+beta*h,sW)
w = dnorm(y[t],h1,sV)
w = w/sum(w)
h = sample(h1,size=M,replace=T,prob=w)
hs = cbind(hs,h)
}
# Quantiles
q025 = function(x){quantile(x,0.025)}
q975 = function(x){quantile(x,0.975)}
h025 = apply(hs,2,q025)
h975 = apply(hs,2,q975)
sd = sqrt(apply(hs,2,var))
m = colMeans(hs)
plot(y,type="b",col="blue",xlab="Time",ylab="y_t", lwd=2, bty='n')
lines(m,col="red")
lines(h025,col="grey",lty=2)
lines(h975,col="grey",lty=2)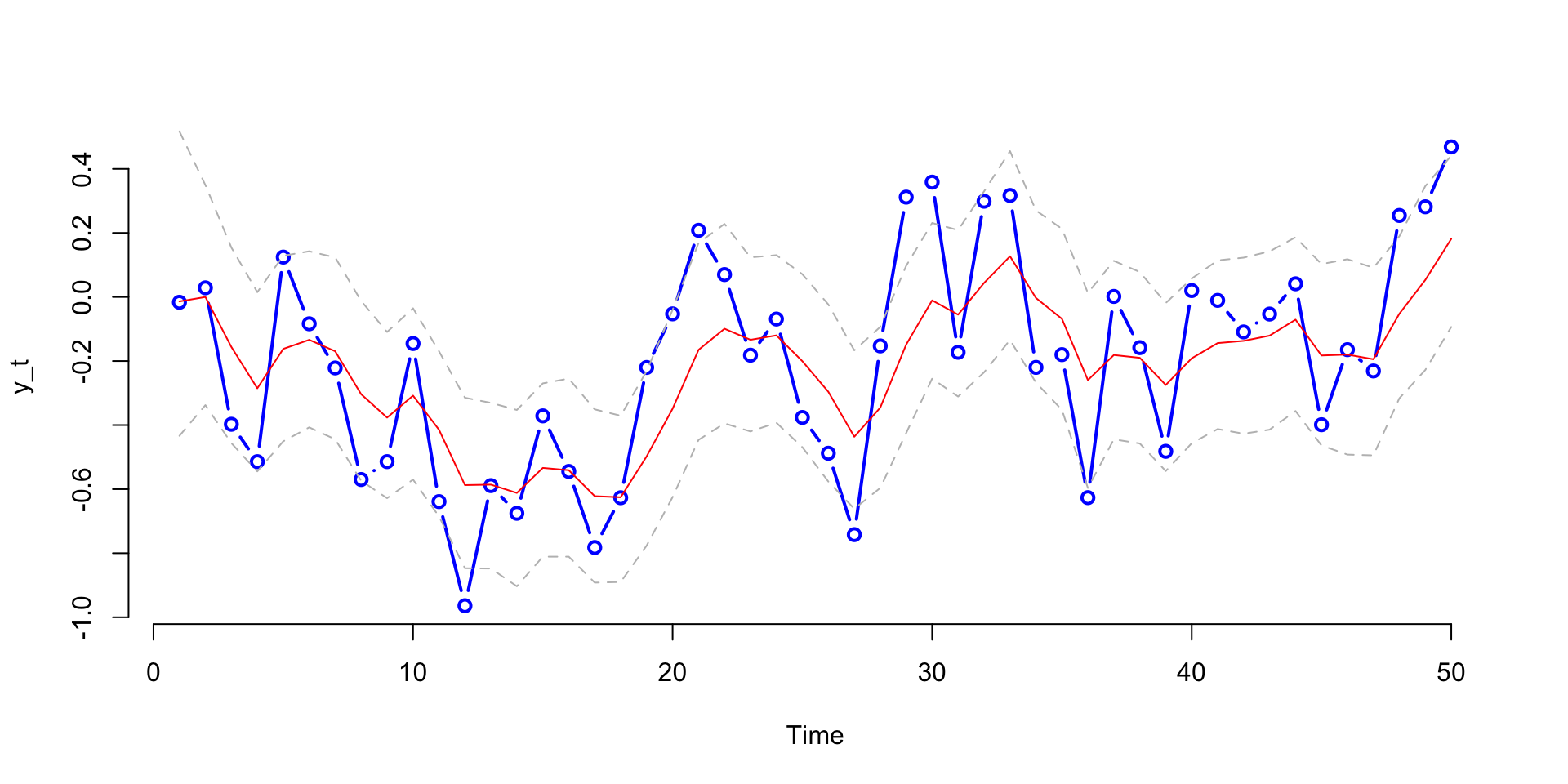
Streaming Data: How do Parameter Distributions change in Time?
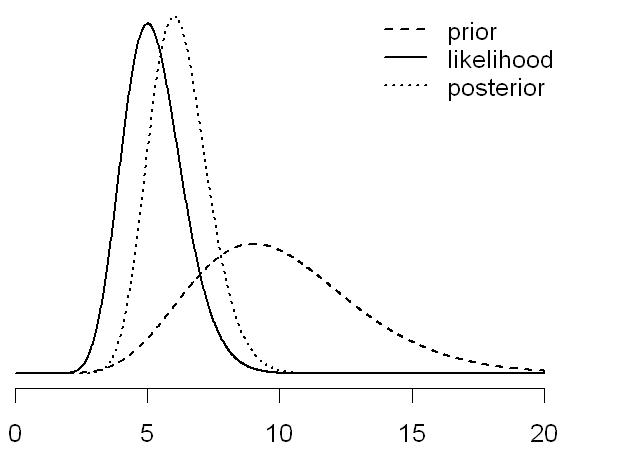 Bayes theorem: \[
p(\theta \mid y^t) \propto p(y_t \mid \theta) \,
p(\theta \mid y^{t-1})
\]
Bayes theorem: \[
p(\theta \mid y^t) \propto p(y_t \mid \theta) \,
p(\theta \mid y^{t-1})
\]
Online Dynamic Learning
- Real-time surveillance
- Bayes means sequential updating of information
- Update posterior density \(p(\theta \mid y_t)\) with every new observation (\(t = 1, \ldots, T\)) - “sequential learning”
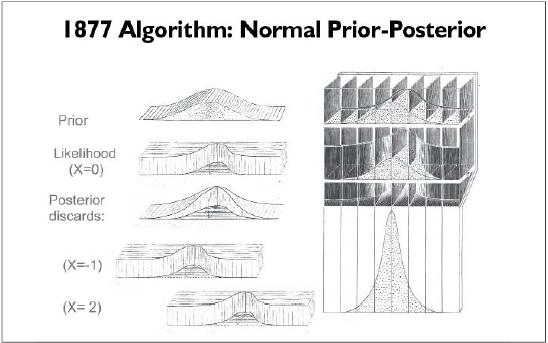
Galton 1877: First Particle Filter
Streaming Data: Online Learning
Construct an essential state vector \(Z_{t+1}\). \[ \begin{aligned} p(Z_{t+1}|y^{t+1}) &= \int p(Z_{t+1}|Z_t, y_{t+1}) \;d\mathbb{P}(Z_t|y^{t+1}) \\ &\propto \int \underbrace{p(Z_{t+1}|Z_t, y_{t+1})}_{propagate} \overbrace{ \underbrace{p(y_{t+1} | Z_t)}_{resample} \;d\mathbb{P}(Z_t|y^t)}\end{aligned} \]
Re-sample with weights proportional to \(p(y_{t+1} | Z_t^{(i)})\) and generate \(\{Z_t^{\zeta(i)}\}_{i=1}^N\)
Propagate with \(Z_{t+1}^{(i)} \sim p(Z_{t+1}|Z_t^{\zeta(i)}, y_{t+1})\) to obtain \(\{Z_{t+1}^{(i)}\}_{i=1}^N\)
Parameters: \(p( \theta | Z_{t+1} )\) drawn “offline”
Sample – Resample
sample-resample
Resample – Sample
resample-sample
Particle Methods: Blind Propagation

Propagate-Resample is replaced by Resample-Propagate
Traffic Problem
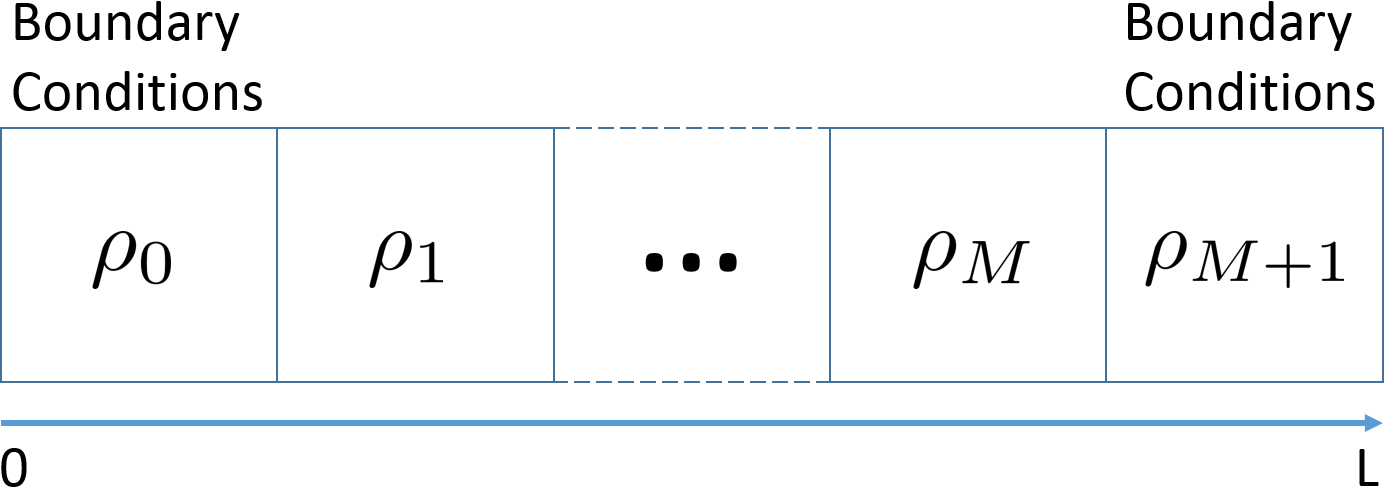
State-Space
Wave Speed Propagation is a Mixture Distribution
Shock wave propagation speed is a mixture, when calculated using Godunov scheme \[
w = \frac{q(\rho_l) - q(\rho_r)}{\rho_l-\rho_r} \ \left[\frac{mi}{h}\right] = \left[\frac{veh}{h}\right]\left[\frac{mi}{veh}\right].
\] Assume \(\rho_l \sim TN(32, 16, 0, 320)\) and \(\rho_r \sim TN(48, 16, 0,320)\)
\(q_c = 1600 \ veh/h\), \(\rho_c = 40 \ veh/mi\), and \(\rho_{jam} = 320 \ veh/mi\)

Traffic Flow Speed Forecast is a Mixtrue Dsitribution
Theorem: The solution (including numerical) to the LWR model with stochastic initial conditions is a mixture distribution.

A moment based filters such as Kalman Filter or Extended Kalman Filter would not capture the mixture.
Problem at Hand
The Parameter Learning and State Estimation Problem
Goal: given sparse sensor measurements, find the distribution over traffic state and underlying traffic flow parameters \(p(\theta_t, \phi|y_1, y_2,...,y_t); \ \phi=(q_c,\rho_c)\)
Parameters of the evolution equation (LWR) are stochastic
Distribution over state is a mixture
Can’t use moment based filters (KF, EKF,...)
Data Assimilation: State Space Representation

State space formulation allows to combine knowledge from analytical model with the one from field measurements, while taking model and measurement errors into account
State Space Representation
State vector \(\theta_t = ( \rho_{1t} , \ldots , \rho_{nt} )\)
Boundary conditionals \(\rho_{0t}\) and \(\rho_{(n+1)t}\)
Underlying parameters \(\phi = (q_c, \rho_c)\) are stochastic
\[\begin{align} \mbox{Observation: }&y_{t+1} = H\theta_{t+1} + v; \ v \sim N(0,V) \label{eqn-y}\\ \mbox{Evolution: }&\theta_{t+1} = f_{\phi}(\theta_t) + w; \ w \sim N(0,W) \label{(eqn-x)} \end{align}\]
\(H: \mathbb{R}^{M} \rightarrow \mathbb{R}^k\) in the measurement model. \(\phi = (q_c,\rho_c, \rho_{max})\).
Parameter priors: \(q_c \sim N(\mu_q, \sigma_c^2)\), \(\rho_c = Uniform(\rho_{min}, \rho_{max})\)
Particle Parameter Learning

Sample-based PDF Representation
Regions of high density: Many particles and Large weight of particles
Uneven partitioning
Discrete approximation for continuous pdf
\[ p^{N}\left( \theta_{t+1}|y^{t+1}\right) \propto \sum_{i=1}^{N}w_{t}^{\left( i\right) }p\left( \theta_{t+1}|\theta_t^{\left( i\right) },y_{t+1}\right) \]
Particle Filter
Bayes Rule: \[ p(y_{t+1},\theta_{t+1}|\theta_t)=p(y_{t+1}|\theta_t)\,p(\theta_{t+1}|% \theta_t,y_{t+1}). \]
- Given a particle approximation to \(p^{N}\left( \theta_t|y^{t}\right)\) \[ \begin{aligned} p^{N}\left( \theta_{t+1}|y^{t+1}\right) & \propto\sum_{i=1}^{N}p\left( y_{t+1}|\theta_t^{\left( i\right) }\right) p\left( \theta_{t+1}|\theta_t^{\left( i\right) },y_{t+1}\right) \label{Mixture2}\\ & =\sum_{i=1}^{N}w_{t}^{\left( i\right) }p\left( \theta_{t+1}|\theta_t^{\left( i\right) },y_{t+1}\right) \text{,}% \end{aligned} \] where
\[ w_{t}^{\left( i\right) }=\frac{p\left( y_{t+1}|\theta_t^{\left( i\right) }\right) }{\sum_{i=1}^{N}p\left( y_{t+1}|\theta_t^{\left( i\right) }\right) }\text{.}% \]
- Essentially a mixture Kalman filter
Particle Parameter Learning
Given particles (a.k.a. random draws) \((\theta^{(i)}_t,\phi^{(i)},s^{(i)}_t),\) \(i=1,\ldots,N\) \[ p( \theta_t | y_{1:t} ) = \frac{1}{N} \sum_{i=1}^N \delta_{ \theta^{(i)} } \; . \]
First resample \((\theta^{k(i)}_t,\phi^{k(i)},s^{k(i)}_t)\) with weights proportional to \(p(y_{t+1}|\theta^{k(i)}_t,\phi^{k(i)})\) and \(s_t^{k(i)}=S(s^{(i)}_t,\theta^{k(i)}_t,y_{t+1})\) and then propogate to \(p(\theta_{t+1}|y_{1:t+1})\) by drawing \(\theta^{(i)}_{t+1}\,\)from \(p(\theta_{t+1}|\theta^{k(i)}_t,\phi^{k(i)},y_{t+1}),\,i=1,\ldots,N\).
Next we update the sufficient statistic as
\[ s_{t+1}=S(s_t^{k(i)},\theta^{(i)}_{t+1},y_{t+1}), \] for \(i=1,\ldots,N\), which represents a deterministic propogation.
- Finally, parameter learning is completed by drawing \(\phi^{(i)}\) using \(p(\phi|s^{(i)}_{t+1})\) for \(i=1,\ldots,N\).
Streaming Data: Online Learning
Construct an essential state vector \(Z_{t+1}\). \[ \begin{aligned} p(Z_{t+1}|y^{t+1}) &= \int p(Z_{t+1}|Z_t, y_{t+1}) \;d\mathbb{P}(Z_t|y^{t+1}) \\ &\propto \int \underbrace{p(Z_{t+1}|Z_t, y_{t+1})}_{propagate} \overbrace{ \underbrace{p(y_{t+1} | Z_t)}_{resample} \;d\mathbb{P}(Z_t|y^t)} \end{aligned} \]
Re-sample with weights proportional to \(p(y_{t+1} | Z_t^{(i)})\) and generate \(\{Z_t^{\zeta(i)}\}_{i=1}^N\)
Propagate with \(Z_{t+1}^{(i)} \sim p(Z_{t+1}|Z_t^{\zeta(i)}, y_{t+1})\) to obtain \(\{Z_{t+1}^{(i)}\}_{i=1}^N\)
Parameters: \(p( \theta | Z_{t+1} )\) drawn “offline”
Resample – Propagate
Algorithm
These ingredients then define a particle filtering and learning algorithm for the sequence of joint posterior distributions \(p( \theta_t , \phi | y_{1:t} )\): \[ \begin{aligned} & \text{Step 1. (Resample) Draw an index } k_t \left( i\right) \sim Mult_{N}\left( w_{t}^{\left( 1\right) },...,w_{t}^{\left( N\right) }\right), \\ & \mbox{where the weights are given by } w_t^{(i)} \propto p(y_{t+1}|(\theta_t,\phi)^{(i)}), \ \text{ for }i=1,...,N\\ \text{ } & \text{Step 2. (Propagate) Draw }\theta_{t+1}^{\left( i\right) }\sim p\left( \theta_{t+1}|\theta_t^{k_t \left( i\right) },y_{t+1}\right) \text{ for }i=1,...,N.\\ \text{ } & \text{Step 3. (Update) } s_{t+1}^{(i)} =S(s_t^{k_t(i)},\theta_{t+1}^{(i)},y_{t+1})\\ \text{ } & \text{Step 4. (Replenish) } \phi^{(i)} \sim p( \phi | s_{t+1}^{(i)} ) \end{aligned} \] There are a number of efficiency gains from such an approach, e.g. it does not suffer from degeneracy problems associated with traditional propagate-resample algorithms when \(y_{t+1}\) is an outliers.
Obtaining state estimates from particles
- Any estimate of a function \(f(\theta_t)\) can be calculated by discrete-approximation
\[ \mbox{E}(f(\theta_t)) = \dfrac{1}{N}\sum_{j=1}^{N}w_t^{(j)}f(\theta_t^{(j)}) \]
- Mean:
\[ \mbox{E}(\theta_t) = \dfrac{1}{N}\sum_{j=1}^{N}w_t^{(j)}\theta_t^{(j)} \]
MAP-estimate: particle with largest weight
Robust mean: mean within window around MAP-estimate
Particle Filters: Pluses
Estimation of full PDFs
Non-Gaussian distributions (multi-modal)
Non-linear state and observation model
Parallelizable
Particle Filters: Minuses
Degeneracy problem
High number of particles needed
Computationally expensive
Linear-Gaussian assumption is often sufficient
Applications: Localization
Track car position in given road map
Track car position from radio frequency measurements
Track aircraft position from estimated terrain elevation
Collision Avoidance (Prediction)
Applications: Model Estimation
Tracking with multiple motion-models
Recovery of signal from noisy measurements
Neural Network model selection (on-line classification)
Applications: Other
Visual Tracking
Prediction of (financial) time series
Quality control in semiconductor industry
Military applications: Target recognition from single or multiple images, Guidance of missiles
Reinforcement Learning
Mixture Kalman Filter For Traffic
\[ \begin{aligned} \mbox{Observation: }&y_{t+1} = Hx_{t+1} + \gamma^Tz_{t+1} + v_{t+1} , \ v_{t+1} \sim N(0, V_{t+1})\\ \mbox{Evolution: }&x_{t+1} = F_{\alpha_{t+1}}x_t + (1-F_{\alpha_{t+1}})\mu + \alpha_t\beta_{t} + \omega_{1} \\ &\beta_{t+1} = \max(0,\beta_{t} + \omega_{2} \label{eqn-beta})\\ \mbox{Switching Evolution: }&\alpha_{t+1} \sim p(\alpha_{t+1} |\alpha_{t},Z_{t}) \end{aligned} \] where \(z_t\) is an exogenous variable that effects the sensor model, \(\mu\) is an average free flow speed \[ \alpha_t \in \{0,1,-1\} \] \[ \omega = (\omega_{1}, \omega_{2})^T \sim N(0, W), \ v \sim N(0,V) \] \[ F_{\alpha_t} = \left\{ \begin{aligned} &1, \ \alpha_t \in \{1,-1\}\\ &F, \ \alpha_t = 0\end{aligned} \right. \] No boundary conditions estimation is needed. No capacity/critical density is needed.