It is remarkable that a science which began with the consideration of games of chance should have become the most important object of human knowledge. Laplace, Pierre Simon, 1812
Data collected by early telescopes played a crucial role in the development of statistical techniques during the 18th century, just as Internet and mobile devices do in the 21st. Massive astronomical data sets inspired scientists such as Carl Friedrich Gauss, Pierre-Simon Laplace, and Sim{'e}on Denis Poisson to devise data-driven methods, including the method of least squares and the Poisson distribution. These methods not only revolutionized astronomy but are also used nowadays in various fields, such as physics, engineering, and economics. The development of these methods marked a significant shift in the scientific approach, enabling more rigorous analysis and interpretation of observational data. The integration of data and statistical methods laid the foundation for modern data science and statistics, demonstrating the power and versatility of data-driven approaches.
In the 18th and 19th centuries data collection was often limited to manual measurements or observations, and the amount of available data was typically much smaller compared to the massive datasets encountered in modern data science. Scientists like Gauss and Poisson often conducted carefully designed experiments, collected their own data, and performed manual calculations without the aid of computers or advanced statistical software. The focus of their work was often on theoretical developments in mathematics, physics and astronomy, and the data was used to test and validate their theories. We can consider one of those studies from the early 18th century.
Example 10.1 (Boscovich and Shape of Earth) The 18th century witnessed heated debates surrounding the Earth’s precise shape. While the oblate spheroid model - flattened poles and bulging equator - held sway, inconsistencies in measurements across diverse regions fueled uncertainty about its exact dimensions. The French, based on extensive survey work by Cassini, maintained the prolate view while the English, based on gravitational theory of Newton (1687), maintained the oblate view.
The determination of the exact figure of the earth would require very accurate measurements of the length of a degree along a single meridian. The final answer to this debate was given by Roger Boscovich (1711-1787) who used geodetic surveying principles and in collaboration with English Jesuit Christopher Maire, in 1755, they embarked on a bold project: measuring a meridian arc spanning a degree of latitude between Rome and Rimini. He employed ingenious techniques to achieve remarkable accuracy for his era, minimizing errors and ensuring the reliability of his data. In 1755 they published “De litteraria expeditione per pontificiam ditionem” (On the Scientific Expedition through the Papal States) that contained results of their survey and its analysis. For more details about the work of Boscovich, see Altić (2013). Stigler (1981) gives an exhaustive introduction to the history of regression.
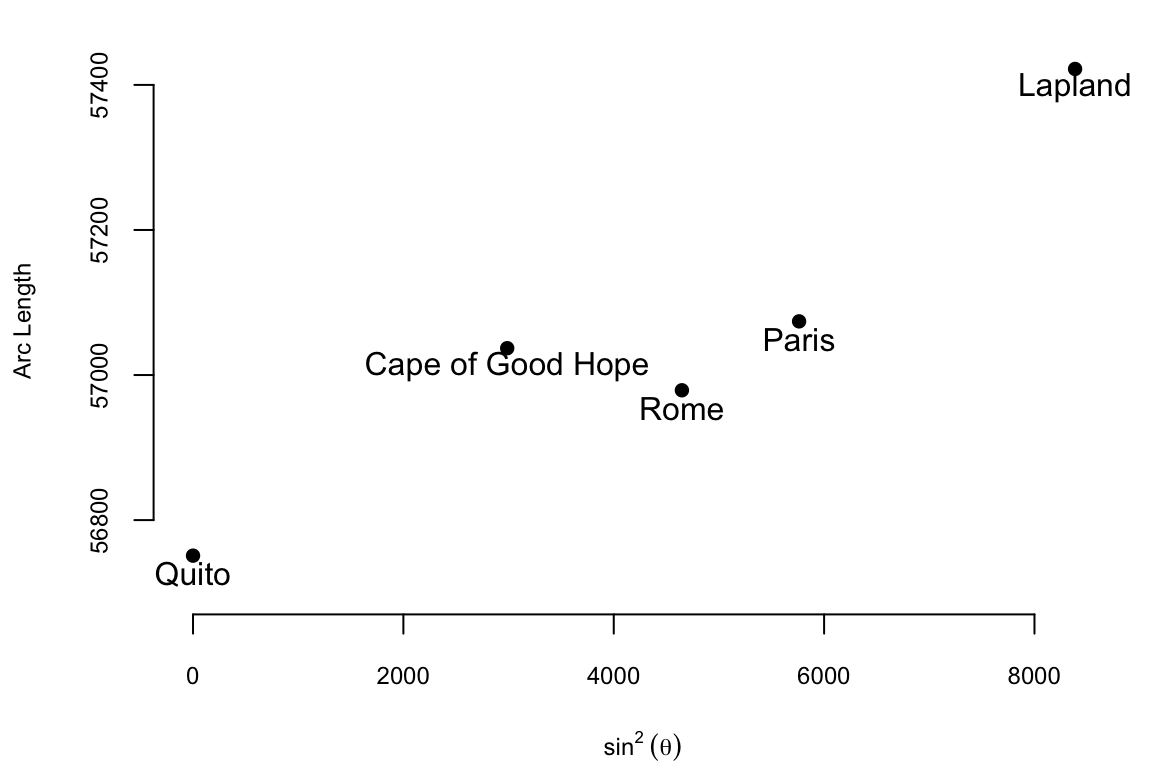
The data on meridian arcs used by Boscovich was crucial in determining the shape and size of the Earth. He combined data from five locations:
d=read.csv("../data/boscovich.csv")
knitr::kable(d, digits = 8)| Location | Latitude | ArcLength | sin2Latitude |
|---|---|---|---|
| Quito | 0 | 56751 | 0 |
| Cape of Good Hope | 33 | 57037 | 2987 |
| Rome | 43 | 56979 | 4648 |
| Paris | 49 | 57074 | 5762 |
| Lapland | 66 | 57422 | 8386 |
plot(d$sin2Latitude,d$ArcLength, ylab="Arc Length", xlab=expression(sin^2~(theta)), pch=16,ylim=c(56700,57450), xlim=c(-30,8590))
text(d$sin2Latitude,d$ArcLength-25, labels=d$Location)
The arc length is measured in toises, a pre-metric unit of about 6.39 feet. Both the table and the plot show that arc length increases with latitude and that its relationship to \(\sin^{2}\theta\) is approximately linear: \[ \text{Arc Length} = \beta_0 + \beta_1 \sin^2 \theta \] where \(\theta\) is the latitude. Here \(\beta_0\) is the length of a degree of arc at the equator, and \(\beta_1\) is how much longer a degree of arc is at the pole. The question that Boscovich asked is how can we combine those five data points to estimate the parameters \(\beta_0\) and \(\beta_1\)? His first attempt to answer this question involved calculating ten slopes for each pair of points and then averaging them. The table below shows the ten slopes.
d = read.csv("../data/boscovich.csv")
sl = matrix(NA,5,5)
for (i in 1:5) {
for(j in 1:(i-1)) {
dx = d$sin2Latitude[i] - d$sin2Latitude[j]
dy = d$ArcLength[i] - d$ArcLength[j]
sl[i,j]=dy/dx
}
}
rownames(sl) = d$Location
colnames(sl) = d$Location
options(knitr.kable.NA = '')
knitr::kable(sl, digits = 4)| Quito | Cape of Good Hope | Rome | Paris | Lapland | |
|---|---|---|---|---|---|
| Quito | |||||
| Cape of Good Hope | 0.096 | ||||
| Rome | 0.049 | -0.035 | |||
| Paris | 0.056 | 0.013 | 0.085 | ||
| Lapland | 0.080 | 0.071 | 0.118 | 0.13 |
Ten slopes for each pair of the five cities from the Boscovich data
plot(d$sin2Latitude,d$ArcLength, ylab="Arc Length", xlab=expression(sin^2~(theta)), pch=16)
text(d$sin2Latitude,d$ArcLength-25, labels=d$Location)
for (i in 1:4){
for (j in (i+1):5){
slope = (d$ArcLength[i] - d$ArcLength[j])/(d$sin2Latitude[i] - d$sin2Latitude[j])
intercept = d$ArcLength[i] - slope*d$sin2Latitude[i]
abline(a=intercept, b=slope)
}
}
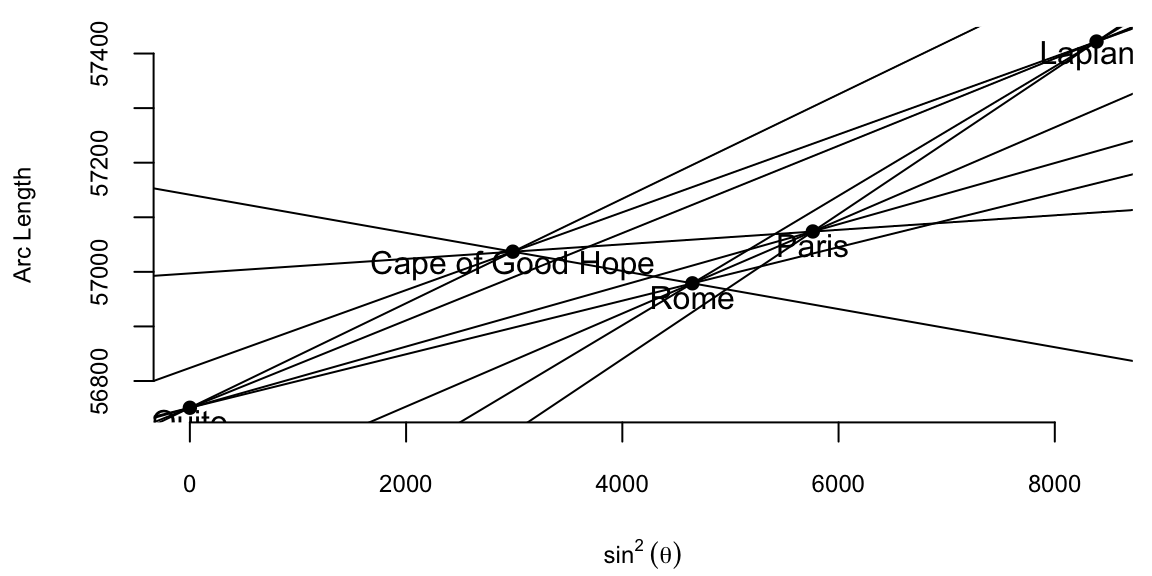
The average of the ten slopes is 0.0667. Notice the slope between Cape of Good Hope and Rome is negative. This is due to the measurement error. Boscovich then calculated an average after removing this outlier. The average of the remaining nine slopes is 0.078. In both cases he used length of the arc at Quito as estimate of the intercept \(\beta_0\). Figure 10.1 (a) shows the line that corresponds to the parameter estimates obtained by Boscovich. Figure 10.1 (b) is the same plot but with the modern least squares line.
d=read.csv("../data/boscovich.csv")
plot(d$sin2Latitude,d$ArcLength, ylab="Arc Length", xlab=expression(sin^2~(theta)), pch=16,ylim=c(56700,57450), xlim=c(-30,8590))
abline(56751,0.06670097, lwd=3, col="red")
plot(d$sin2Latitude,d$ArcLength, ylab="Arc Length", xlab=expression(sin^2~(theta)), pch=16,ylim=c(56700,57450), xlim=c(-30,8590))
abline(lm(ArcLength~sin2Latitude, data=d), lwd=3, col="red")
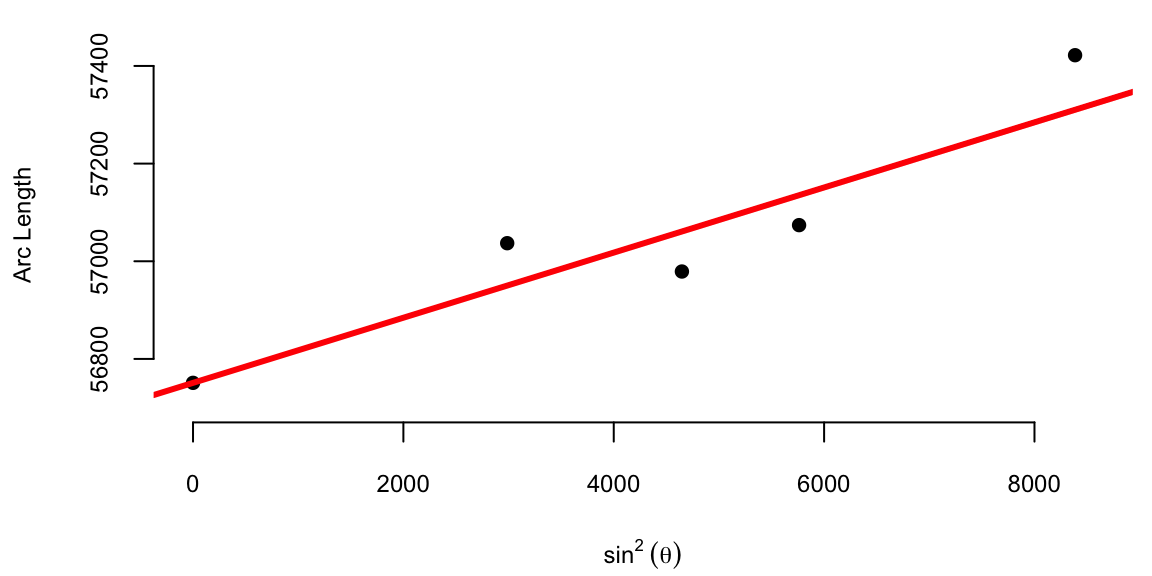
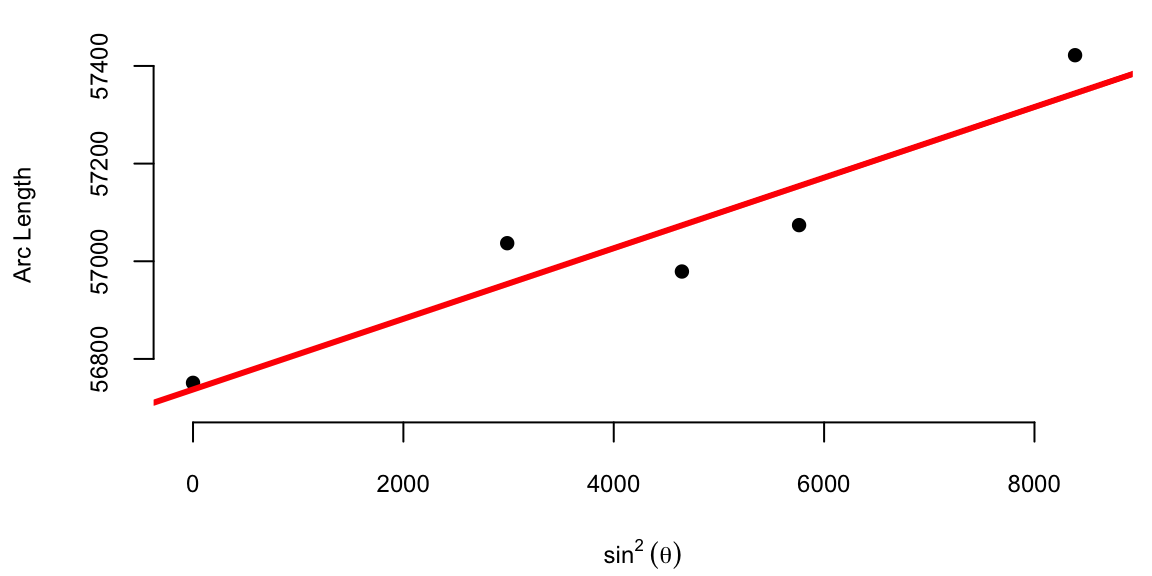
This is a very reasonable approach! However, Boscovich was not satisfied with this approach and he wanted to find a better way to combine the data. He was looking for a method that would minimize the sum of the absolute deviations between the data points and the fitted curve. Two years later he developed a pioneering technique called least absolute deviations, which revolutionized data analysis. This method, distinct from the prevalent least squares approach, minimized the sum of absolute deviations between data points and the fitted curve, proving particularly effective in handling measurement errors and inconsistencies.
Armed with his meticulous measurements and innovative statistical analysis, Boscovich not only confirmed the oblate spheroid shape of the Earth but also refined its dimensions. His calculations yielded a more accurate value for the Earth’s equatorial radius and the flattening at the poles, providing crucial support for Newton’s theory of gravitation, which predicted this very shape.
Motivated by the analysis of planetary orbits and determining the shape of the Earth, later in 1805, Adrien-Marie Legendre (1752-1833) published the first clear and concise explanation of the least squares method in his book “Nouvelles m{'e}thodes pour la d{'e}termination des orbites des cometes”. The method of least squares is a powerful statistical technique used today to fit a mathematical model to a set of data points. Its goal is to find the best-fitting curve that minimizes the sum of the squared distances (also known as residuals) between the curve and the actual data points. Compared to the approach proposed by Boscovich, the least squares method is less robust to measurement errors and inconsistencies. However, from a computational point of view, it is more efficient and various algorithms exist for efficient calculation of curve parameters. This computational efficiency is crucial for modern data analysis, where datasets can be massive and complex, making least squares a fundamental tool in statistics and data analysis, offering a powerful and widely applicable approach to data fitting and model building.
Legendre provided a rigorous mathematical foundation for the least squares method, demonstrating its theoretical underpinnings and proving its optimality under certain conditions. This mathematical basis helped establish the credibility and legitimacy of the method, paving the way for its wider acceptance and application. Legendre actively communicated his ideas and collaborated with other mathematicians, such as Carl Friedrich Gauss (1777-1855), who also contributed significantly to the development of the least squares method. While evidence suggests Gauss used the least squares method as early as 1795, his formal publication came later than Legendre’s in 1809. Despite the delay in publication, Gauss independently discovered the method and applied it to various problems, including celestial mechanics and geodesy. He developed efficient computational methods for implementing the least squares method, making it accessible for practical use by scientists and engineers. While Legendre’s clear exposition and early publication brought the least squares method to the forefront, Gauss’s independent discovery, theoretical development, practical applications, and contributions to computational methods were equally crucial in establishing the method’s significance and impact. Both mathematicians played vital roles in shaping the least squares method into the powerful statistical tool it is today.
Another French polymath Pierre-Simon Laplace (1749-1827) extended the methods of Boscovich and showed that the curve fitting problem could be solved by ordering the candidate slopes and finding the weighted median. Besides that, Laplace made fundamental contributions to probability theory, developing the Bayesian approach to inference. Most of Laplace’s work was in the field of celestial mechanics, where he used data from astronomical observations to develop mathematical models and equations describing the gravitational interactions between celestial bodies. His analytical methods and use of observational data were pioneering in the field of celestial mechanics. Furthermore, he developed methods for estimating population parameters from samples, such as the mean and variance and pioneered the use of random sampling techniques, which are essential for ensuring the validity and generalizability of statistical inferences. These contributions helped lay the foundation for modern sampling theory and survey design, which are crucial for conducting reliable and representative studies. Overall, Laplace’s contributions to data analysis were profound and enduring. His work in probability theory, error analysis, sampling methods, and applications significantly advanced the field and laid the groundwork for modern statistical techniques. He also played a crucial role in promoting statistical education and communication, ensuring that these valuable tools were accessible and utilized across various disciplines.
Boscovich used what we call today a linear regression analysis. This type of analysis relies on the assumption that the relationship between the independent (sine squared of the latitude) and dependent (arc length) variables is linear. Francis Galton was the person who coined the term “regression” in the context of statistics. One of the phenomena he studied was the relationship between the heights of parents and their children. He found that the heights of children tended to regress towards the average height of the population, which led him to use the term “regression” to describe this phenomenon. Galton promoted a data-driven approach to research that continues to shape statistical practice today. Furthermore, he introduced the concept of quantiles, which divide a population into equal-sized subpopulations based on a specific variable. This allowed for a more nuanced analysis of data compared to simply considering the mean and median. He also popularized the use of percentiles, which are specific quantiles used to express the proportion of a population below a certain value.
Galton used regression analysis to show that the offspring of exceptionally large or small seed sizes of sweet peas tended to be closer to the average size. He also used it for family studies and investigated the inheritance of traits such as intelligence and talent. He used regression analysis to assess the degree to which these traits are passed down from parents to offspring.
Galton’s overall approach to statistics was highly influential. He emphasized the importance of quantitative analysis, data-driven decision-making, and empirical research, which paved the way for modern statistical methods and helped to establish statistics as a recognized scientific discipline.
There are many modern applications of using data to solve problems. We will discuss one of them.
Example 10.2 (Formula One) As described in the Artificial Intelligence in Formula 1 article, Formula One teams are increasingly leveraging AI and machine learning to optimize race strategies. The article highlights how teams collect massive amounts of data during races - with 300 sensors per car generating millions of data points over 200-mile races. This data includes critical variables like fuel load, tire degradation, weight effects, and pit stop timing that must be optimized in real-time.
The key innovation is moving from pre-race strategy planning to in-race dynamic optimization using cloud computing platforms like AWS. Teams run Monte Carlo simulations of all cars and traffic situations to continuously update their strategy recommendations. This allows them to make optimal decisions about when to pit, which tires to use, and how to manage fuel consumption based on real-time race conditions rather than static pre-race plans.
The article emphasizes that the best strategies can vary dramatically from moment to moment during a race, making real-time AI-powered decision making crucial for competitive advantage. Teams are limited to 60 data scientists, so they must rely heavily on automated machine learning systems to process the vast amounts of sensor data and generate actionable insights during races.
The CNBC article highlights how Formula One championships are increasingly being determined by technological innovation rather than just driver skill. F1 success depends heavily on advanced data analytics, machine learning algorithms, and real-time computing capabilities. Key technological factors driving F1 success include real-time data processing where teams process millions of data points from hundreds of sensors per car during races. AI-powered strategy optimization uses machine learning algorithms to continuously analyze race conditions and recommend optimal pit stop timing, tire choices, and fuel management. Cloud computing infrastructure allows teams to rely on platforms like AWS to run complex simulations and data analysis during races. Predictive modeling employs advanced algorithms to predict tire degradation, fuel consumption, and competitor behavior. Simulation capabilities enable teams to run thousands of Monte Carlo simulations to optimize race strategies.
The technological arms race in Formula One has led to significant regulatory challenges. To maintain competitive balance and prevent larger teams from gaining insurmountable advantages through unlimited technological investment, F1 has implemented strict caps on the number of engineers and data scientists that teams can employ. Currently, teams are limited to 60 data scientists and engineers, which forces them to be highly strategic about their technological investments and resource allocation. This cap creates an interesting dynamic where teams must balance the need for sophisticated AI and machine learning capabilities with the constraint of limited human resources. As a result, teams are increasingly turning to automated systems and cloud-based solutions to maximize their technological capabilities within these constraints. The cap also levels the playing field somewhat, ensuring that success depends more on the efficiency and innovation of the technology rather than simply having more engineers and data scientists than competitors.